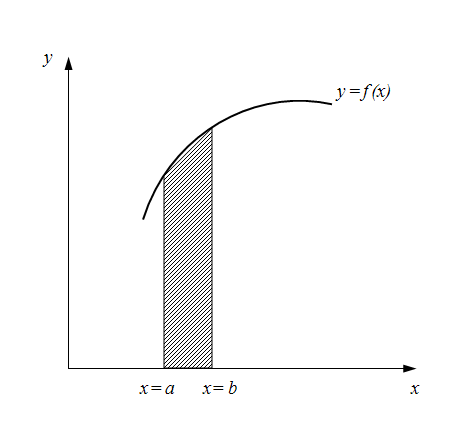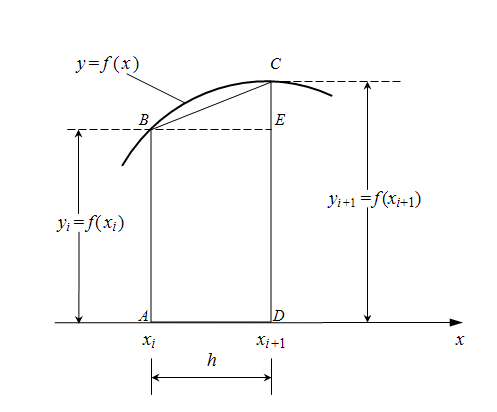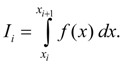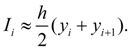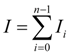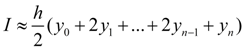The trapezoid rule

Let's consider the integral (2) representing, as is known, area under a curve on segment (Fig. 1).

Fig. 1. Geometrical representation of numerical integration

Let's break now interval of integration  ( a , b )  to n equal parts in length everyone ( h is called step of integration ). We’ll consider one of these intervals (Fig. 2).

Fig. 2. One interval of numerical integration by trapezoid method

The area under a curve between is equal:

Let's assume, that the step of integration h is small enough then this area without an essential error can be equated to the area of trapezoid ABCD . As , we’ll receive:

(3)

As integral from sum is equal to sum of integrals (property of additivity ), then

,      (4)

where .

Substituting (3) in (4), we’ll finally receive [3, 4]:

.       (5)

It also is the formula of trapezes . The trapezoid rule – one of elementary methods of numerical integration and though an error of calculations in this way has more, than in other methods, it is in great demand owing to its presentation and simplicity.