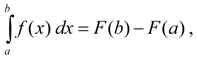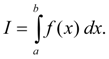Introduction

In engineering practice constantly there is a necessity of calculation of definite integrals. If some function is continuous on segment and its primitive is known, the definite integral from this function can be calculated from Newton-Leibniz formula:

(1)

where

However in most cases there are no final formulas expressing indefinite integral in form of  combination of elementary functions as to find primitive it is not obviously possible. In cases when probably to express integral analytically, received final formula often happens is so complex for calculations [1, 2], that it is more convenient to integrate function numerically, having received the approached value of integral. Besides in practice integrand is often given tabular and then calculation of integral analytical by in general loses sense.

Numerical integration is region of approached methods of calculation of definite integrals. There is a set of methods of numerical integration: the trapezoid rule, Simpson's, Gauss's, Newton-Leibniz, Chebishev's formulas etc. We’ll be limited here to consideration of two most simple and widely applied algorithms: the trapezoid rule and Simpson’s method.

So, let it is required to calculate the definite integral:

(2)

where – integrand; function, continuous on segment .

The problem of numerical integration consists in calculation of value of integral (2) on a number of values of integrand .