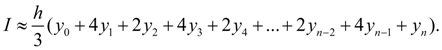Simpson’s rule

Simpson's rule – one of widest known and applied methods of numerical integration. It is similar to rule of trapezes as also is based on splitting of general interval of integration into fineer segments. However its difference that for calculation of area through each three consecutive ordinates of splitting the square parabola is spent. Lowering needless details and calculations we’ll result a final kind of Simpson’s formula [3, 4]:

(6)

Here n is an even number. This formula is much more exact than trapezoid formula. So, at integration of polynomials of degree not above third Simpson's method gives exact values of integral.