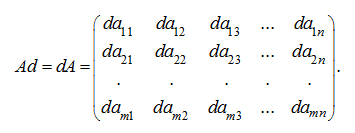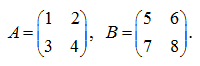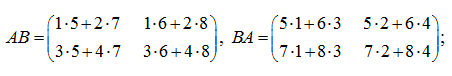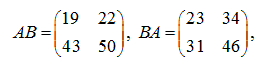Operations with matrices

1. Equality of matrices

Two matrices 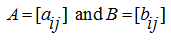of the same dimensions 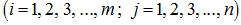are considered equal: А = В , if their appropriating elements are equal, that is

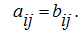
2. The sum and difference of matrices

The sum of two matrices 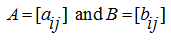of the same dimensions 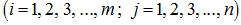is called the matrix 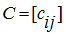of the same dimension which elements are equal to the sum of appropriating elements of the matrices A and B .

From the definition of the sum of matrices its basic properties directly follow:
1) А+В = В+А ;
2) А+( В+С ) = ( А+В )+С ;
3) А + 0 = А .

The difference of matrices A and B is defined similarly.

3. Multiplication of a matrix to number

The product of a matrix A on number d (or product of number d on a matrix A ) is called the matrix, which elements are products of a matrix A elements on a number d . Differently,

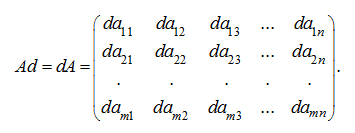
From the definition of product of number on a matrix its basic properties directly follow:
1)  1 А = А 1= А ;
2)  0 А = А 0=0 ;
3) d ( hA ) = ( dh ) A = h ( dA ) ;
4)  ( d+h ) A=dA+hA ;
5) d ( A+B ) = dA+dB .

Here A and B – matrices, d and h – numbers.

Let's notice, that for the order n square matrix A the equality takes place:
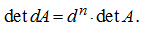
The matrix – A = (–1) A is called opposite . Apparently, that for two matrices A and B of an identical dimension the equality takes place: A – B = A + (– B ).

4. Multiplication of matrices

Let dimensions of matrices A and B are equal accordingly to m × n and n × k , that is the number of columns of a matrix A is equal to number of rows of a matrix B , then for these two matrices the matrix C of  dimension m × k is certain, being their product: C = АВ . Elements of a matrix C are calculated under the formula:

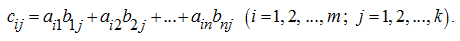
From here it follows, that the element costing in i-th row and j-th column of a matrix-product, is equal to the sum of products of elements of i-th row of the first matrix on appropriating elements of j-th column of the second matrix.

From the definition of product of matrices it follows, that it is possible to multiply square matrices only of the same orders .

The basic properties of matrix product:
1) А ( ВС ) = ( АВ ) С ;
2) d ( АВ ) = ( dA ) B ;
3)  ( А+В ) С= АС+ ВС ;
4) С ( А+В ) = СА+ СВ .

Here A , B and C – matrices, d – a number.

The product of two matrices generally is not commutative , that is AB ≠ BA . In that specific case, when AB = BA , matrices A and B are called commutative (permutable). As it is easy to make sure, an identity matrix E is commutative with any square matrix of the same order, and AE = EA = A . Consequently, at multiplication of matrices an identity matrix E plays the same role, that unit at multiplication of numbers.

For square matrixes A and B of the same orders the equality takes place: det ( AB ) = det ( BA ) = det A · det B .

E x a m p l e .  The matrices are given

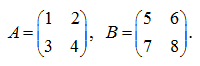
Calculate determinants of left and right products АВ and ВА .

S o l u t i o n .

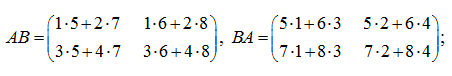
or it is final:

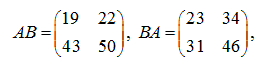
that is AB ≠ BA .

However, determinants of products АВ and ВА are equal:
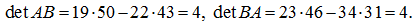