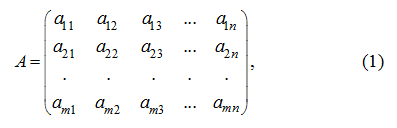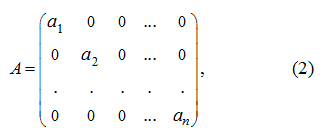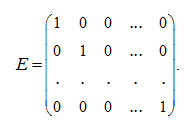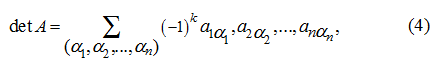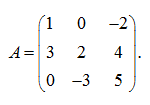The basic definitions

System from mn numbers (real, complex), either functions, or other objects, recorded in the form of the rectangular table consisting from m rows and n columns:

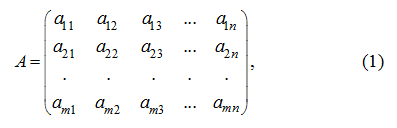
is called matrix .

Numbers (functions, other objects) 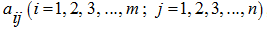, making the matrix (1), are called elements of a matrix . Here the first index i designates the row number, and the second j – the column number on intersection of which the given element of a matrix is located.

For a matrix (1) there is a shorthand record:

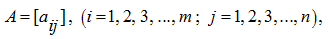
or simply 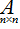. In this case speak, that the matrix A has dimension m×n . If m=n the matrix is called square of the order n . If m≠n the matrix is called rectangular . The matrix of dimension 1 ×n is called a vector-row, and a matrix of dimension m× 1 – a vector-column. It is possible to consider usual number (scalar) as a matrix of dimension 1 × 1.

If the square matrix looks like:

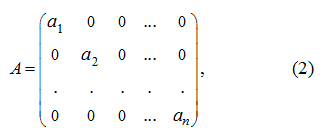
then it is called diagonal matrix.

If in the diagonal matrix (2) all diagonal elements are equal to1 then this matrix is called identity matrix and is designates as:

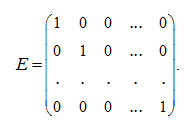
Using Kronecker’s symbol

it is possible to record:

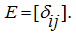
The matrix at which all elements are equal to 0 is called zero matrix and is designated 0.

Elements of the n -th order square matrix 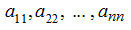form a so-called main diagonal of a matrix .
The sum of elements of the main diagonal is called a trace or a spur of a matrix :

The concept determinant is connected with a square numerical matrix:

Matrix and its determinant different (though and connected) concepts. The numerical matrix A is the ordered system of numbers recorded in the form of the rectangular table, and its determinant det A is the number equal:

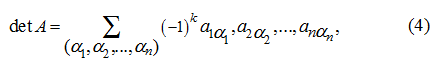
where the sum (4) extends on possible permutations 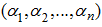of elements 1, 2..., n and, consequently, contains n !  addends, and k = 0, if the permutation is even and k = 1, if the permutation is odd.

E x a m p l e .  Calculate a determinant of a matrix

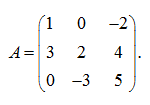
S o l u t i o n .  According to (3) we have:
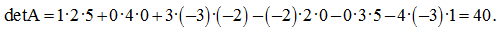