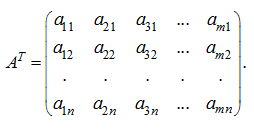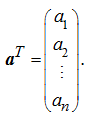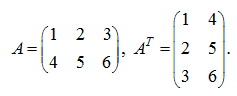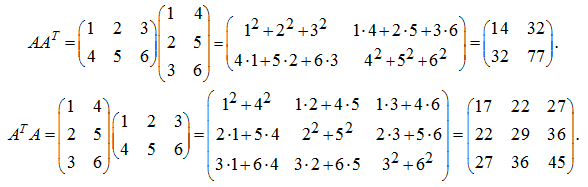The transposed matrix

Replacement of rows by columns in a matrix of dimension m × n

gives the so-called transposed matrix of dimension n × m :

In particular, for a vector-row the transposed matrix is the vector-column

The basic properties of the transposed matrix:
1) twice transposed matrix coincides with initial matrix:

2) the transposed matrix of the sum of matrices is equal to the sum of the transposed matrix addends, that is

3) the transposed matrix of the product of matrices is equal to the product of the transposed matrix factors, taken upside-down:

For a square matrix the obvious equality takes place:

If the matrix coincides with the transposed one, that is

then it is called symmetric . From this equality follows, that the symmetric matrix is square, and its elements are symmetric concerning the main diagonal, are equal among themselves:

Apparently, that the product is a symmetric matrix as, using property 3, we’ll receive:

E x a m p l e .  The matrix A and the transposed matrix are given:

Calculate the products and .

S o l u t i o n .

As one would expect, the symmetric matrices have been received.