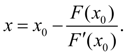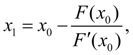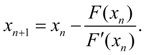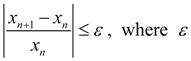Method of tangents (Newton-Raphson method)

Let's consider again the equation (1):

(1)

where F ( x ) – is a differentiated function, defined in the interval

Let's expanse the function F ( x ) in a power series and we’ll be limited to a linear part of expansion:

(5)

that is equivalent to exchanging of function F ( x ) in any point x to its tangent in this point.

Then from (1) and (5) follows:

(6)

If to accept for zero approach, the formula (6) can be used for a finding of the following, the 1-st approach:

(7)

From here it follows, that the ( n + 1) approach will be defined under the formula:

(8)

The correlation (8) also is a method of tangents or Newton-Raphson method .

The conditions convergence for process (8) looks like:

1) zero approach is chosen close enough to a root of the equation

2) derivative F" ( x ) does not become too big,

3) derivative F’ ( x ) is not too close to 0.

The last condition means, that no two roots existed the close one from another, and joint performance of conditions 2) and 3) is similar to the requirement in a method of iterations .

The process (8) is considered completed, if – the given accuracy of the solution.

Newton-Raphson method finds a wide application for the solution of the high order systems of nonlinear equations. You can see examples here and here .