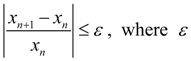Method of iterations (method of consecutive approximations)

An iterative process converges , if at performance of consecutive iterations we receive values of roots, all closer and closer coming nearer to exact value of a root. Otherwise, an iterative process is considered diverging.

Let's copy for convenience the equation (1) in the form of:

(3)

That it is possible to receive by exchanging: .

Let – zero approach, i.e. the initial approached value of a root of the equation (3). Then as the following, the 1-st approach we’ll accept

the following, the 2-nd approach will be

etc., as the n -th approach we’ll accept

(4)

Here there is a main question: whether comes nearer to the true solution of the equation (3) at unlimited increasing n ? Differently, whether the iterative process (4) converges?

The convergence conditions of a method of iterations [2]: if at all values calculated from solving process (4):

1) , then an iterative process converges;

2) , then an iterative process diverges.

If in some points the derivative on the module is less than 1, and in other points it is greater than 1, to tell anything certain about convergence of iterative process impossible. It can both to converge, and to diverge.

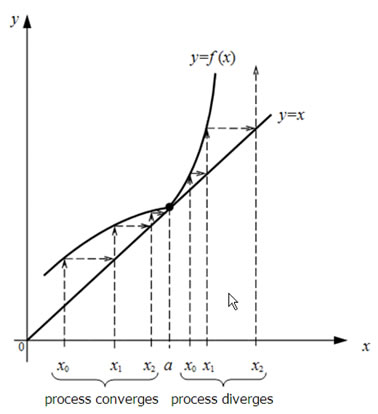
If an iterative process diverges, the reason of it often is the unsuccessful choice of zero approach. So, on Fig.1 it is shown, that the choice of zero approach essentially influences convergence of an iterative process. It directly is connected with, whether there is a zero approach in the field of where the conditions of convergence of iterative process are satisfied.

Fig.1. Dependence of iterative process convergence on a choice of zero approach

The process (4) is considered completed, if – the given accuracy of the solution.