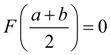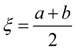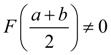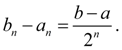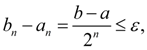Method of halving

Let's consider the equation (1):

where F ( x ) – is a continuous function, defined in the segment and

The last means, that function F ( x ) has into the segment at least one root. Let's consider a case, when the root into the segment is unique.

We halve the segment. If , then is the root of the equation (1). If , then we consider that half of the segment on which ends function F ( x ) has different signs. The new, narrower segment we again halve and spent it on the same consideration and so on. As a result on some step we’ll receive either exact value of a root of the equation (1), or sequence of the segments enclosed each other:

such, that

(9)

and

(10)

The left ends of these segments form the monotonous (not decreasing) limited sequence, and the right ends – the monotonous (not increasing) limited sequence. Therefore by equality (10) there is a general limit

Passing in (9) to a limit at , by continuity of the function F ( x ) we’ll receive: Hence, that is is a root of the equation (1).

In practice the process (10) is considered completed, if

(11)

where – the given accuracy of solution.