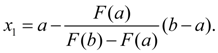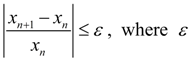Method of chords (method of proportional parts)

Again we’ll address to the equation (1):

where F ( x ) – is a continuous function, defined in the segment and

There is faster way of a finding of the isolated root of equation (1), lying in the segment. Let's assume for definiteness, that Instead of the segment halving, we’ll divide it relation It gives the first approach of a root of the equation (1):

(12)

Then we consider the segments . Let's choose that from them, on which ends the function F ( x ) has different signs, then we’ll receive the second approach of a root of the equation (1) and so on until then yet we’ll not reach performance of an inequality – the given accuracy of the decision. Geometrically this method is equivalent to exchanging the curve у = F ( x ) with a chord, lead at first through the points and then with chords, lead through the ends of received segments (Fig. 2). From here the name – a method of chords .

Fig.2. Geometrical representation of a method of chords.