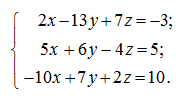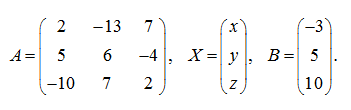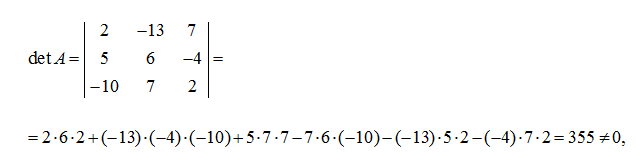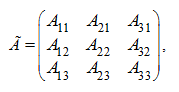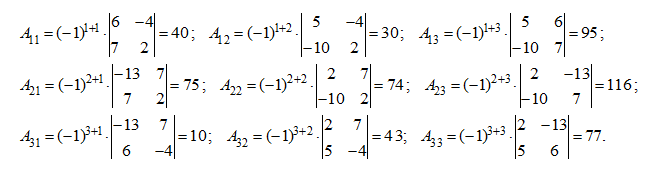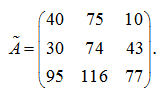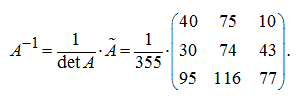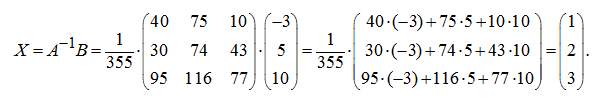Example

Solve the system of linear equations, using the matrix methods:

S o l u t i o n

Let's record the given system of linear equations in the matrix form:

where

The solution of the given system of linear equations in the matrix form looks like:

where – an inverse matrix to a matrix A .

The determinant of the matrix A of coefficients is equal:

consequently, the matrix A has an inverse matrix .

First we’ll find an adjoint matrix à which in the given example looks like:

where – algebraic additions of appropriating elements of matrix A .

In our case we’ll receive:

Thus,

Then the inverse matrix is equal:

Now we’ll find the solution of the given system of equations. As, then

Thus, the solution of the given system of equations: