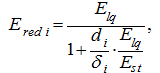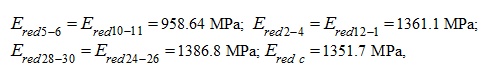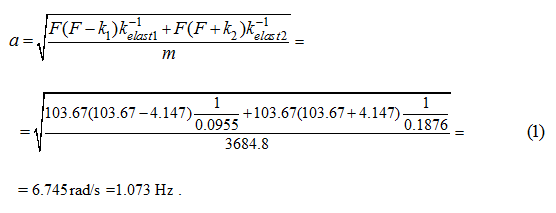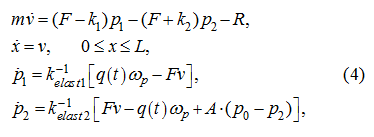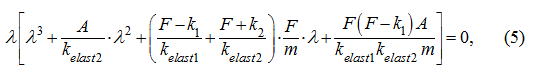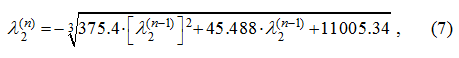Contents >> Engineering Mathematics >> Control Systems >> Dynamic Synthesis of Control System of Hydraulic Drive >> Synthesis of control by a power hydraulic drive of volumetric regulation >> Method of multiple periods of natural vibrations >> Example

Control Systems - Dynamic Synthesis - Method of multiple periods of natural vibrations - Example

Example

The algorithm of control offered in the previous section we'll consider on the specific rated diagram of a hydraulic drive of progress with the closed circulation of a stream (Fig. 5), modeling transients in hydraulic system by means of the program of dynamic calculation of any diagrams of volumetric hydraulic drive HYDRA. (see the section "Hydraulic Systems. Dynamic Analysis").

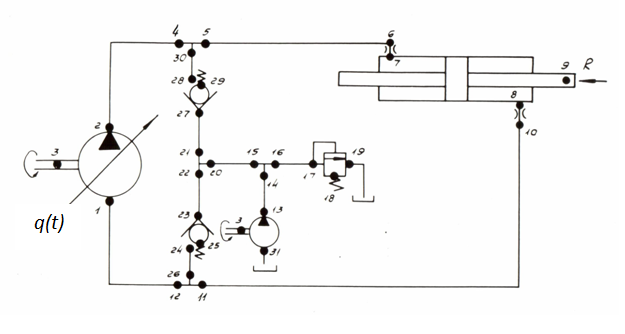
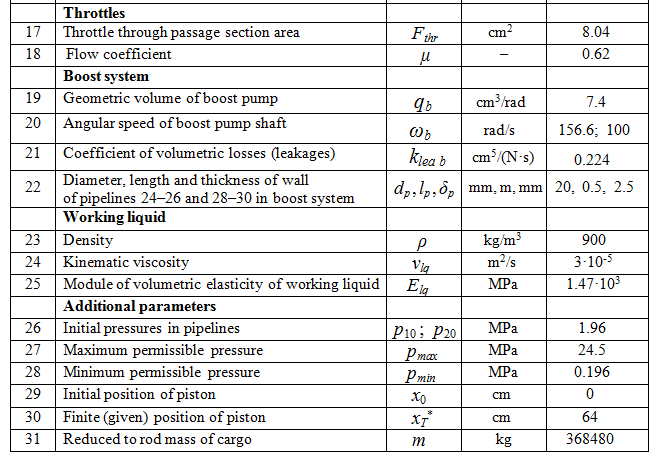
Fig. 5.

As all necessary parameters of control ( Т I , Т II , Т III , q p , ... ) are calculated in advance and involved in the program of formation of external indignations PERTR, check of offered algorithm of control by numerical experiment (which objective to establish a degree of adequacy of the accepted key points) as in system HYDRA varied nonlinear communications of elements and parameters of a hydraulic drive are considered in most general view, such as is in essence realized: variable elasticity of cavities of the hydraulic cylinder, loss of pressure on length of pipelines and in local resistances, outflow of a working liquid from cavities of the pump, work of system of additional charging on dynamics of return valves, etc.
Before to estimate a degree of influence of this or that factor on parameters of control (mainly, on the lowest natural frequency of hydraulic system), we'll consider main parameters of hydraulic system presented in tab. 1.

The reduced modules of elasticity of pipelines 5 – 6, 10 – 11, 2 – 4, 12 – 1, 28 – 30, 24 – 26 and cavities of the hydraulic cylinder (all – with a working liquid) are defined according to the formula (7) previous sections "Algorithm"

where d i , δ i – diameter and thickness of a wall of i -th cavity; Е lq – the module of volumetric elasticity of working liquid; Е st – the module of elasticity of a cavity wall material. The following values of the resulted modules of elasticity are as a result received:

whence according to the formula (6) previous sections "Algorithm" we'll receive following values of factors of elasticity of pressure head and drain highways in the beginning of a course of the piston of the hydraulic cylinder:

Factors of proportionality of making forces of friction in cavities of the hydraulic cylinder k 1 and k 2 are equal [10, 11]:

then according to the equations (9) – (10) previous sections "Algorithm"

or

natural frequency of hydraulic system is equal:

Modeling hydraulic system (Fig. 5) by the program HYDRA gives value of frequency of natural fluctuations 6 rad/s. In the Appendix it is shown, that taking into account variable elasticity of hydraulic system, losses of pressure on length of pipelines, in local resistance and leakages practically do not change eigenvalues of hydraulic system. Thus, a difference between values of natural frequency (at calculation "manually" a = 6.75 rad/s, at modeling by the program HYDRA a = 5.5...6 rad/s) can be explained by oscillation property of boost system which at an assessment "manually" was not considered. Therefore we’ll accept for the further a = 6 rad/s. Then according to conditions of (32) previous sections "Algorithm"

To check the condition (36) previous sections "Algorithm" for a drain pipeline is not necessary here, as at any choice n fulfillment of the condition (35) is provided with boost system that proves to be true results of modeling (see further). As during movement of the hydraulic cylinder piston k elast 1 increases, it is meaningful to admit to the given case n = 1, instead of 2 and by that twice to reduce time of dispersal Т I :

Check of an inequality (50) previous sections "Algorithm": gives:

Thus, it is final Т I = 1.05 s.
As the considered hydraulic system (Fig. 5) is symmetric, we'll accept Т III = Т I = 1.05 s, then according to expression (49) previous sections "Algorithm" :

consequently, total time of regulation
On Fig. 6 results of numerical experiment – modeling of transients in considered hydraulic system by means of the program HYDRA in using control with the parameters found above are resulted.

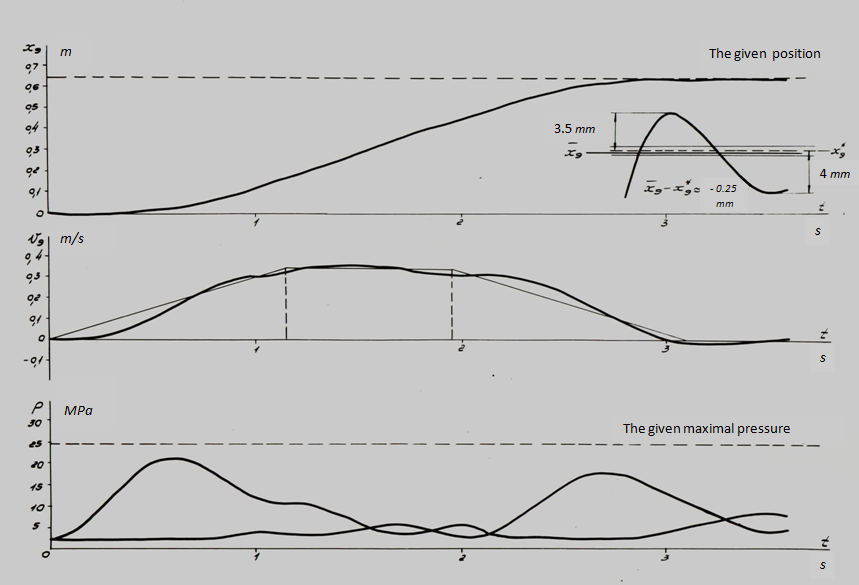
Fig. 6.

Here diagrams of variation in time of movement х 9 and speed v 9 of the hydraulic cylinder piston (node 9 on Fig. 6), pressure р 1 and р 2 (accordingly in nodes 1 and 2), as well as set trapezoidal dependence q (t), reduced to type:

are presented. Apparently from Fig. 6, it is not possible to extinguish completely natural fluctuations of system at an appearance on a mode of the "steady-state" movement. Besides after the end of control fluctuations of the hydraulic cylinder piston relatively some position of the balance , which differs from the target point х 9 * = 64 cm at ~ 3.7 mm. That is, accuracy of positioning at completely damped vibrations of the hydraulic cylinder piston makes about 4 mm. The beginning of control process (0 ≤ t ≤ Т I ) is characterized over-pressure р 2 up to 28 MPa, exceeding the set level of the maximal pressure (25 MPa) on ~ 12%. The specified deviations from character and parameters of transient at the chosen strategy of control take place on two principal causes: availability of essentially nonlinear effects (including influence of boost system, inconstancy of elastic properties in process of moving the piston) as a result of which frequency of natural fluctuations "floats", as well as some computing discrepancies in definition of parameters of control (for example, it was accepted n = 1 though actually the right part of an inequality (32) the previous section "Algorithm" in this case was equaled ~ 1.052), that has led to a little bit overestimated peak of pressure р 2 , etc. For specification of parameters of control by hydraulic system for the 2-nd version of calculation angular speed of the basic pump shaft has been accepted ω н = 100 rad/s, whence that is n = 1, consequently, still

Then Т = 1.05 + 0.9 + 1.05 = 3 s. Results of calculation (computer modeling) are presented on Fig. 7.

Fig. 7.

Here, as well as earlier, v 9 , х 9 – speed and movement of the hydraulic cylinder piston (node 9), р 1 , р 2 – pressure in input and output of the basic pump (nodes 1 and 2). In comparison with the 1-st rated case the significantly better agreement of the given and actual parameters of control process is observed. So, over-pressure р 2 in the given rated case was equal to ~ 23 MPa, error of positioning is less about three (a deviation of the established position of the piston from the given one х 9 * = 64 cm have made ~ 1.3 mm), an oscillation property of transients has decreased. Improvement of parameters of control process is reached due to an insignificant increase of time Т II and general time of regulation Т (in this case Т = 3 s in comparison with 2.605 s in the previous example). However here again natural fluctuations are traced neatly, to extinguish which completely it is not possible. Last circumstance as already it was marked above, is connected with availability nonlinearities in considered hydraulic system (variable rigidity, oscillation property of boost system, etc.), not considered at synthesis of parameters of the control, lead on linear model. Nevertheless "hit" in a vicinity of a target point of positioning х 9 * with a margin error ε ≈ 1.3 mm for the given type of control (without introduction of correcting links with feedback by position, speed, etc.) can be considered as comprehensible. Increase of accuracy of positioning, including improvement damping properties of hydraulic system can be achieved really due to introduction of "precise" control by means of in appropriate way chosen correcting links.
As already it was marked above, in the Appendix it is shown, that the account of variable factors of elasticity, losses of pressure on length of pipelines and in local resistances, leakages of working liquid almost does not influence on values of natural frequencies, however existing differences in character and numerical values of parameters of considered transients (planned values at synthesis of control and "actual" values at numerical experiment) testify to an indispensability of the account of boost system at construction of algorithm of control, at least a level of the task of the static characteristic of boost return valves. Therefore let's consider one more rated case, and natural frequency of hydraulic system we'll define in view of the static characteristic of the return valve in boost system. For this purpose the equation of flows [see the system of equations (5) in the previous section "Algorithm" ] in a drain pipeline of the hydraulic system we'll write in the form of:

where Q b – boost flow through the return valve equal according to its static characteristic:

where A – angular factor of the static characteristic, р 0 – pressure in the boost system.

In view of (2) and (3) the mathematical model of dynamics of hydraulic system at dispersal at operation of the return valve in the boost system will become:

then we'll receive the following characteristic equation:

solving which, we'll receive eigenvalues of the considered hydraulic system. It is easy to see, that at A = 0 (that is without taking into account the return valve in the boost system) we'll receive the equation which decision is (1). Generally the characteristic equation (5) has roots: λ 1 = 0, appropriating a constant component of transient, also three roots of the cubic equation solved usually numerically. Using values of parameters of the hydraulic system (tab. 1), we'll receive the following characteristic equation:

whence λ 1 = 0.
It is known, that among roots of the cubic equation, at least, one – real. We'll find it by iterative method :

where – value λ 2 on n -th iteration.
With accuracy ε = 0.001 required root is equal λ 2 = – 375.357 and conforms a rapidly damped component of proper decision of the equations (4) (time constant ~ 0.003). Eigenvalues defining oscillation property of system, are found from the quadratic equation received by division of the polynomial (6) on the binomial λ ( λ + 375.357 ) :

λ 2 + 0.043 λ + 29.348 = 0,     (8)

λ 3,4 ≈ – 0.0215 ± 5.42 i ,   (9)

whence a natural frequency of the hydraulic system is equal а = 5.42 rad/s = 0.862 Hz. The found value practically coincides with the least observed one (5.46 rad/s) as a result of modeling dynamics of the hydraulic system by the program HYDRA. The factor of damping ν = 0.0215 testifies underdamping of natural fluctuations (logarithmic decrement in this case makes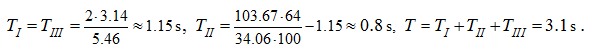 ). Consequently, on the one hand there is fair an assessment of transient on simplified model (16) – (18) previous sections "Algorithm" , and with another – a consideration of one more rated version for which parameters of control are equal: а = 5.46 rad/s, ω p = 100 rad/s is of interest; then on conditions (32) and (50) previous sections "Algorithm" : and whence n = 1, and therefore,

Results of modeling of the last rated version are resulted on Fig. 8.

Fig. 8.

Here required accuracy of positioning of 0.5 mm is received(a deviation of an equilibrium position of the hydraulic cylinder piston from the given х 9 * = 64 cm have made 0.25 mm), however because of small damping of the hydraulic system oscillatory processes after the end of regulation process (t > T) take place. Over-pressures do not exceed the given level.
The considered examples show, that at a stage of "rough" control realization of the offered algorithm of multiple periods of natural fluctuations, is possible in the main, however an availability of some essentially nonlinear effects does not allow determining a natural frequency of hydraulic system enough precisely. So, changeability of elastic properties of drive in process of movement of the hydraulic cylinder piston leads to variation of frequency of natural fluctuations, and means, that the actual system is not completely adequate to linear model with constant factors. Besides a hydraulic system with volumetric regulation is slightly damped. Therefore for achievement of high accuracy of positioning it is necessary:
1) to increase a damping degree of a hydraulic drive;
2) to enter correcting links at a stage of "precise" control with feedback by position and speeds of the piston, and it may be - on acceleration (pressures in the hydraulic cylinder cavities).
It is not excluded, that the decision of both problems can be reached by introduction of appropriating feedback.


< Previous Contents Next >