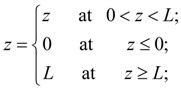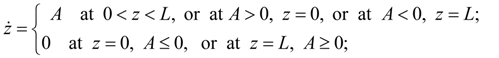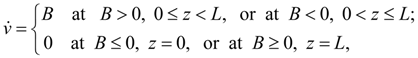Library of mathematical models of typical linear dynamic links

In control systems various physical devices are used: hydraulic, electromagnetic, electro hydraulic, etc. Therefore at the solution of problems of dynamics of systems it is necessary to simulate control and regulation systems various by their nature. The majority of them is well described by means of typical linear dynamic links of automatic control [1] to which the following links are related:

1) an ideal intensifying (no inertial) link – an adder;

2) the 1-st order aperiodic (inertial) link;

3) the 2-nd order aperiodic link;

4) an oscillatory link;

4a) a conservative link (a special case of an oscillatory link);

5) an ideal integrating link;

6) an inertial integrating link;

7) an ideal differentiating link;

8) an ideal link with introduction of derivative;

9) an inertial differentiating link;

10) the 2-nd order dynamic link (the general case).

Mathematical models of the listed linear dynamic links are written in the form of ordinary differential equations, instead of in operational form (in the form of transfer functions) as transient processes are interested for us in time area, instead of in frequency area.

Generally the 2-nd order linear dynamic link is described by the equation:

(2)

where signals on input of the link; their time derivatives; х – signal on output of the link; coefficients of the equation.

For all other types of dynamic links their equations are received as special cases (2):

an ideal intensifying (no inertial) link – an adder:

(2.1)

the 1-st order aperiodic (inertial) link:

(2.2)

the 2-nd order (aperiodic or oscillatory) link:

(2.3)

a conservative link:

(2.4)

an ideal integrating link:

(2.5)

an inertial integrating link:

(2.6)

an ideal differentiating link:

(2.7)

an ideal link with introduction of derivative:

(2.8)

an inertial differentiating link:

(2.9)

Thus, all typical linear links can be incorporated in one generalized element the LINK (the identifier of this element in library of base elements) with nodes i (input), j (output), k (an additional input for the link – adder).

Conditions, restrictions, comments. It is necessary to add the resulted equations of linear dynamic links by some restrictions reflecting physical properties of variables, and also some design features of devices (for example, detents of mobile parts).

In some real elements movement z of mobile parts is limited by detents. Such nonlinearity can be written in the form of inequalities:

(3)

(4)

(5)

where L – a maximal value of movement z ; А – a right part of the differential equation resolved respect to ; В – a right part of the differential equation resolved respect to .