Partial Differential Equations - solution of the elliptic equation
Example: The solution of the elliptic equation
Dynamics of block of cylinders of axial-piston pump
Let's consider a problem of dynamics of centralized block of cylinders of the axial-piston pump [1]. The simplified diagram is
presented on Fig.2. The block of cylinders in mass
m
rotates with angular speed
ω
concerning a motionless surface of port plate
. Between the block of cylinders and a surface of port plate there is a layer of oil film thickness
h
. From cylinders on the block a
force of pressing down
R
operates, and from an oil film – a force of pushing up
W
operates. Under action of these forces the block
of cylinders makes fluctuations with swing
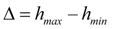 and speed
and speed
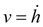 relatively
an average clearance
h
av
. Limiting values of basic parameters of pump: maximal pressure and speed of shaft rotation
depend on value of swing of fluctuations. To define dependence of pushing up force
W
and swing of fluctuations of the block it is
necessary to solve all over again a problem about distribution of pressure in an oil film between surfaces of the block and the port plate
which solution was offered in due time by Dr. R.M.Pasynkov [2]. In essence it is one of many problems of dynamics of hydrostatic sliding saddles
and bearings [3].
relatively
an average clearance
h
av
. Limiting values of basic parameters of pump: maximal pressure and speed of shaft rotation
depend on value of swing of fluctuations. To define dependence of pushing up force
W
and swing of fluctuations of the block it is
necessary to solve all over again a problem about distribution of pressure in an oil film between surfaces of the block and the port plate
which solution was offered in due time by Dr. R.M.Pasynkov [2]. In essence it is one of many problems of dynamics of hydrostatic sliding saddles
and bearings [3].
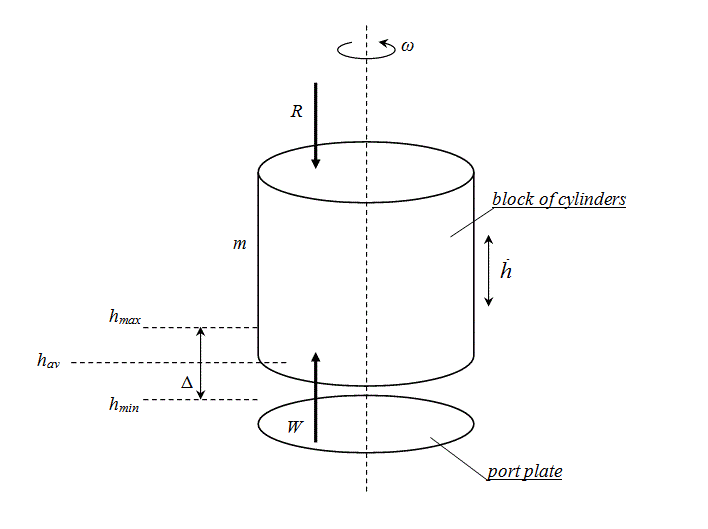
Fig. 2. The simplified diagram of dynamics of the block of cylinders
The equation of the block movement along its axis rotation:
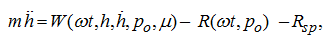 (3)
(3)
where
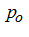 – pressure in pressure head cylinders of the pump,
– pressure in pressure head cylinders of the pump,
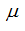 – coefficient of dynamic viscosity of a liquid,
– coefficient of dynamic viscosity of a liquid,
 – the block press force by a spring.
– the block press force by a spring.
It is possible to write down the dependence of pressing down force
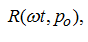 ,
acting on the block from piston apertures of pressure head cylinders, in the form of periodic piece-constant function:
,
acting on the block from piston apertures of pressure head cylinders, in the form of periodic piece-constant function:
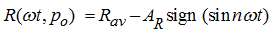 , (4)
, (4)
where
 –
average value and amplitude of fluctuations of pressing down force,
D
– diameter of cylinder,
n
– number of cylinders of the block.
–
average value and amplitude of fluctuations of pressing down force,
D
– diameter of cylinder,
n
– number of cylinders of the block.
For definition of force of pushing up (bearing ability of oil film)
W
it is necessary to find distribution of a field of pressure
p
in oil film which in arbitrary time moment can be described by Reynolds's equation [3]:
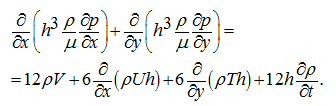 (5)
(5)
Here
U, V, T
– components of the block speed concerning the port plate.
Except for the known assumptions at which the equation (5) is valid, we shall enter a number of additional restrictions, lawful at
the given statement of the problem: the density
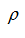 and viscosity
and viscosity
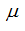 of a liquid in a film are constant in time on all surface of friction; the interfaced surfaces of the block and the port plate at any
moment are equidistant:
of a liquid in a film are constant in time on all surface of friction; the interfaced surfaces of the block and the port plate at any
moment are equidistant:
 ;
value of a solid angle of area of the port plate not more than 45 deg., that allows at calculation of a field of pressures to accept a surface
of the port plate plane. It is easy to show, that for a case of rotary motion concerning axis, a perpendicular plane
ху
, the equality
takes place:
;
value of a solid angle of area of the port plate not more than 45 deg., that allows at calculation of a field of pressures to accept a surface
of the port plate plane. It is easy to show, that for a case of rotary motion concerning axis, a perpendicular plane
ху
, the equality
takes place:
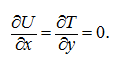 Therefore in view of the accepted assumptions the last three terms in the right part of equation (5) vanish to zero. Then, taking into
consideration that
Therefore in view of the accepted assumptions the last three terms in the right part of equation (5) vanish to zero. Then, taking into
consideration that
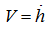 , the equation (5) can be described in polar coordinates
, the equation (5) can be described in polar coordinates
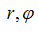 in the form of:
in the form of:
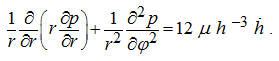 (6)
(6)
This equation describes a field of pressures in an oil film between the port plate and the block which makes fluctuations along axis
of rotation.
At forthcoming of sliding surfaces of the pump block of cylinders and port plate there is an expression of oil film and there is an
additional variable component of pushing up force that is taken into consideration by presence of the right part in the equation (6). The
numerical solution of the equation (6) enables to define in the fixed time moment a field of pressures in oil film and value of bearing
capacity
W
in view of dynamics of the block of cylinders.
For any fixed time moment the right part of the equation (6) accepts the certain value, and the equation becomes the Poisson’s equation.
In that specific case at
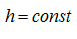 it turns to Laplace’s equation in polar coordinates:
it turns to Laplace’s equation in polar coordinates:
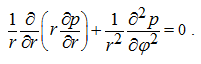 (7)
(7)
Numerical solution of elliptic equations (6) of Poisson and (7) of Laplace at the given boundary conditions can be carried out by
method of finite differences (method of grids).
The solution of the equation (6) by virtue of its linearity is maybe presented as superposition of the solution of the equation (7), which
applied to this problem is known from [2], and the private solution of the equation (6).
The press up force may be presented in the form of:
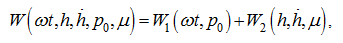 (8)
(8)
where
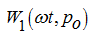 – the press up force component at a constant clearance;
– the press up force component at a constant clearance;
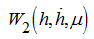 – the press up force dynamical component at a variable clearance.
The solution of the equation (6) has been received by a method of final differences (method of grids). Calculations of
– the press up force dynamical component at a variable clearance.
The solution of the equation (6) has been received by a method of final differences (method of grids). Calculations of
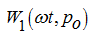 for various angles of turn of the block concerning the port plate have shown, that this value maybe presented in the form of piecewise
constant function of the block turn angle. Constancy pieces correspond to two main positions of the block: either
(
n
– 1) / 2 cylinders of the block are connected to a pressure cavity, or (
n
+ 1) / 2. At turn of the block on angle
within the limits of which the number of cylinders connected to a pressure cavity, does not change, value
for various angles of turn of the block concerning the port plate have shown, that this value maybe presented in the form of piecewise
constant function of the block turn angle. Constancy pieces correspond to two main positions of the block: either
(
n
– 1) / 2 cylinders of the block are connected to a pressure cavity, or (
n
+ 1) / 2. At turn of the block on angle
within the limits of which the number of cylinders connected to a pressure cavity, does not change, value
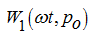 ,
as calculations have shown for five positions of the block, can be considered as a constant. Besides it is possible to consider that
phases of
,
as calculations have shown for five positions of the block, can be considered as a constant. Besides it is possible to consider that
phases of
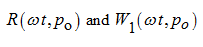 coincide, as speed of propagation of pressure in a liquid film (~1200 m/s) is incommensurable more the block speed. Therefore it’s
possible to assume, that variation of field of pressures and bearing capacity of film at change of number of pressure cylinders occurs
instantly. Consequently,
coincide, as speed of propagation of pressure in a liquid film (~1200 m/s) is incommensurable more the block speed. Therefore it’s
possible to assume, that variation of field of pressures and bearing capacity of film at change of number of pressure cylinders occurs
instantly. Consequently,
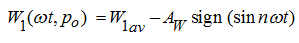
where
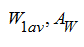 – average value and amplitude of the press up force component
– average value and amplitude of the press up force component
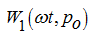 .
.
For reception of functional dependence of the press up force component
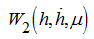 calculations of fields of pressures and bearing capacity have been carried at various values of the right part of the equation (6), i.e.
at variable parameters
calculations of fields of pressures and bearing capacity have been carried at various values of the right part of the equation (6), i.e.
at variable parameters
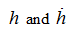 .
With variation of
.
With variation of
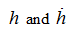 the
the
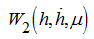 value also changes.
value also changes.
As dependence
 ,
and consequently and
,
and consequently and
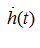 ,
is required, is enough to set approximate value of the equation (6) right part.
,
is required, is enough to set approximate value of the equation (6) right part.
Giving consistently a number of values of the right part of the equation (6), we’ll receive corresponding values of bearing capacity of film
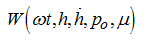 . Having put
. Having put
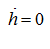 ,
at the motionless block, we’ll receive value of a static component
,
at the motionless block, we’ll receive value of a static component
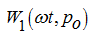 ,
as in this case
,
as in this case
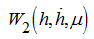 = 0. On the basis of the equation (8) it follows, that the
= 0. On the basis of the equation (8) it follows, that the
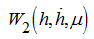 value is defined as a difference between
value is defined as a difference between
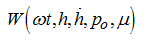 and
and
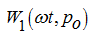 .
Carried numerical calculations have shown, that
.
Carried numerical calculations have shown, that
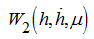 is proportional to the right part of the equation (6) with some coefficient
is proportional to the right part of the equation (6) with some coefficient
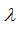 :
:
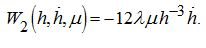 (9)
(9)
The value of the proportionality coefficient
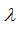 depends on a standard size of the hydrounit and geometry of the port plate. The minus in the right part of the formula (9) results from that
depends on a standard size of the hydrounit and geometry of the port plate. The minus in the right part of the formula (9) results from that
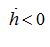 ,
corresponds to rapproachement of the block and the port plate at which
,
corresponds to rapproachement of the block and the port plate at which
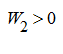 .
.
Thus all components in (3) are received and in view of (4) and (9) this equation will become:
 . (10)
. (10)
The equation (10) is valid at the following two conditions:
1) the indicator diagram of the axial-piston pump is those, that peaks of pressure
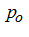 in the jammed volume in a moment of passage of the crosspiece between pressure and drain windows of the port plate is not present practically;
in the jammed volume in a moment of passage of the crosspiece between pressure and drain windows of the port plate is not present practically;
2) friction in the pair piston –cylinder is negligible in comparison with other efforts, acting on the block.
Let's consider preliminary relations
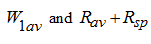 .
Three basic cases which are resulting from a condition of a hydrostatic equilibration of the block are possible.
.
Three basic cases which are resulting from a condition of a hydrostatic equilibration of the block are possible.
a) The case
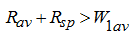 is inadmissible, as thus there will be an expression of a film from a clearance between the block and the port plate, conditions теплоотдачи will
worsen, there will be a danger of wear of slipping surfaces owing to infringement of the film continuity; contact of slipping surfaces of the
block and the port plate is possible.
is inadmissible, as thus there will be an expression of a film from a clearance between the block and the port plate, conditions теплоотдачи will
worsen, there will be a danger of wear of slipping surfaces owing to infringement of the film continuity; contact of slipping surfaces of the
block and the port plate is possible.
b) In the case of
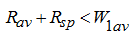 the block is wrung out from the port plate, the clearance increases, that results to increase of outflow and inadmissible decrease in volumetric
efficiency. A design of the port plate, as well as in the first case, is disabled.
the block is wrung out from the port plate, the clearance increases, that results to increase of outflow and inadmissible decrease in volumetric
efficiency. A design of the port plate, as well as in the first case, is disabled.
c) The case
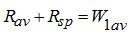 corresponds to stable work of the pump and dynamic equilibration of the block. Thus the equation (10) becomes:
corresponds to stable work of the pump and dynamic equilibration of the block. Thus the equation (10) becomes:
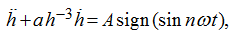 (11)
(11)
where
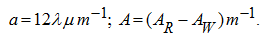
To solve the equation (11) in quadratures because of its essential nonlinearity it is impossible, however it is possible to lower its order
unitary integration:
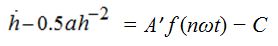 (12)
(12)
where
А' = А/(nω)
,
 - the function, presented on Fig.3
a
.
- the function, presented on Fig.3
a
.
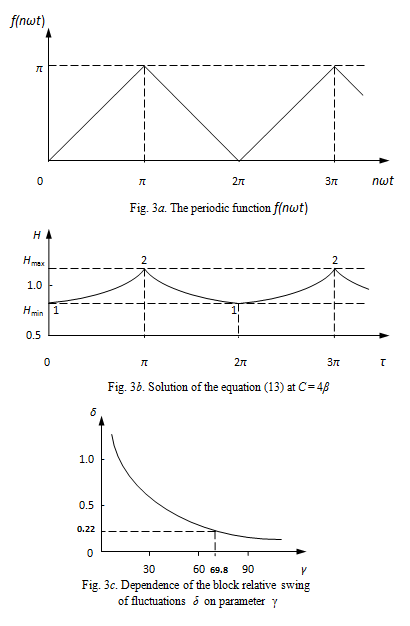
To find the common solution of the equation (12) it's impossible, for reception of private solutions we’ll use a numerical method. We’ll notice,
that values of factors
a
and
A'
differ more than on three orders, therefore it is necessary to result the equation (12) in a
dimensionless type:
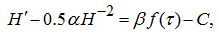 (13)
(13)
where
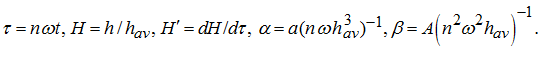 .
.
The equation (13) has been solved numerically for some values of
C
. The received solution
 at
C
= 4
β
(Fig.3
b
) has points of a break 1 and 2 (jump of a derivative) at
at
C
= 4
β
(Fig.3
b
) has points of a break 1 and 2 (jump of a derivative) at
 , that
is there where sign (sin
τ
) changes a sign.
, that
is there where sign (sin
τ
) changes a sign.
If in the equation (13) to neglect
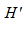 , then the
received algebraic equation
, then the
received algebraic equation
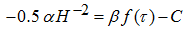
has solutions
 ,
similar on character on dependence on Fig.3
b
with an error, not exceeding 6%. This allows to simplify the equation of dynamics of the
block:
,
similar on character on dependence on Fig.3
b
with an error, not exceeding 6%. This allows to simplify the equation of dynamics of the
block:
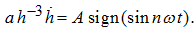
Let's find the periodic solution of this equation by a
method of sewing together
:
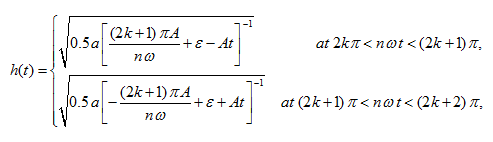 (14)
(14)
where
ε
– an arbitrary constant (
ε
> 0);
k
= 0, 1, 2, … .
From here we find the maximal and minimal values of the film thickness:
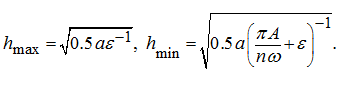 (15)
(15)
From relations (15) in view of designations (11) we’ll receive:
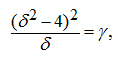 (16)
(16)
where
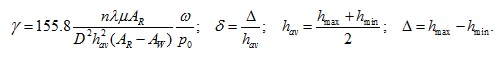
Apparently, that the area of possible variations of relative swing of fluctuations
 ,
therefore a polynomial
,
therefore a polynomial
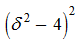 – is a monotonically decreasing function, from here it follows, that
– is a monotonically decreasing function, from here it follows, that
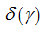 is an univocal function (Fig.3
c
). Thus, for definition
is an univocal function (Fig.3
c
). Thus, for definition
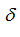 on the
equation (16) the graphical-analytical solution is offered.
on the
equation (16) the graphical-analytical solution is offered.
The value
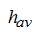 ,
entering into the equation (16), depends on
ω, р
o
, as well as on a standard size of the hydro unit. On the basis of calculations
of bearing capacity for experimental pump-hydro motor MM-1 of VNIIstroydormash (displacement volume is equal to ~ 500 cc
3
/rev,
diameter of piston
D
= 40 mm) the following values of the parameters entering in
γ
have been received:
,
entering into the equation (16), depends on
ω, р
o
, as well as on a standard size of the hydro unit. On the basis of calculations
of bearing capacity for experimental pump-hydro motor MM-1 of VNIIstroydormash (displacement volume is equal to ~ 500 cc
3
/rev,
diameter of piston
D
= 40 mm) the following values of the parameters entering in
γ
have been received:
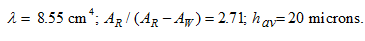 Other input data:
Other input data:
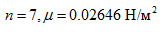 .
At work on a nominal mode
ω
= 105 rad/s (1000 rev/min),
р
o
= 16 MPa. We find
γ
= 69.8. Then from
the equation (16) and Fig. 3
c
we have
.
At work on a nominal mode
ω
= 105 rad/s (1000 rev/min),
р
o
= 16 MPa. We find
γ
= 69.8. Then from
the equation (16) and Fig. 3
c
we have
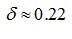 , whence the value of fluctuations swing of the block of cylinders is
, whence the value of fluctuations swing of the block of cylinders is
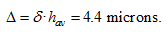 .
The experiments carried on pump-hydro motor MM-1, have allowed receiving the following empirical dependence of an average clearance
.
The experiments carried on pump-hydro motor MM-1, have allowed receiving the following empirical dependence of an average clearance
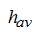 on
ω
and
р
o
:
on
ω
and
р
o
:
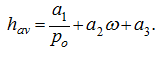 (17)
(17)
Here the following values of coefficients of the equation (17) have been received:
a
1
= 36.7,
a
2
= 0.075,
a
3
= 11.8.
As result on the basis of the dependence (17) and the equation (16) the zones of fluctuations of the block at various modes of operation have been
certain.
The results received on the new design development stage, have allowed to establish limits of possible speeding up of the hydro unit,
to specify its characteristics and the requirements to a filtration of a working liquid.
|
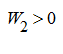 .
.
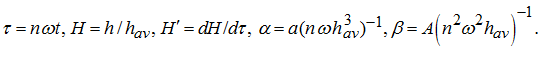 .
.
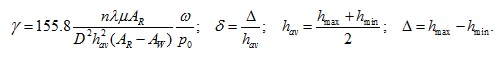
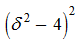 – is a monotonically decreasing function, from here it follows, that
– is a monotonically decreasing function, from here it follows, that

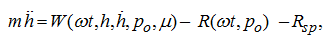 (3)
(3)
 – the block press force by a spring.
– the block press force by a spring.
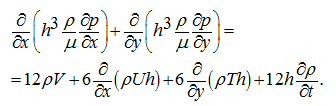 (5)
(5)
 ;
value of a solid angle of area of the port plate not more than 45 deg., that allows at calculation of a field of pressures to accept a surface
of the port plate plane. It is easy to show, that for a case of rotary motion concerning axis, a perpendicular plane
ху
, the equality
takes place:
;
value of a solid angle of area of the port plate not more than 45 deg., that allows at calculation of a field of pressures to accept a surface
of the port plate plane. It is easy to show, that for a case of rotary motion concerning axis, a perpendicular plane
ху
, the equality
takes place:
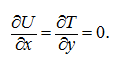 Therefore in view of the accepted assumptions the last three terms in the right part of equation (5) vanish to zero. Then, taking into
consideration that
Therefore in view of the accepted assumptions the last three terms in the right part of equation (5) vanish to zero. Then, taking into
consideration that
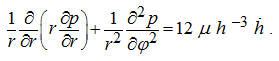 (6)
(6)
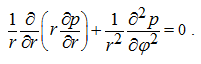 (7)
(7)

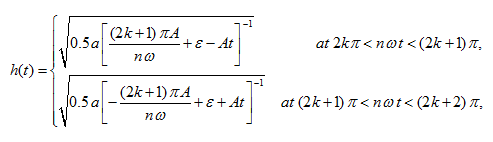 (14)
(14)
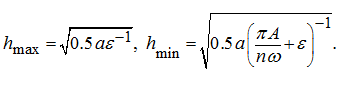 (15)
(15)
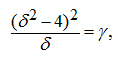 (16)
(16)
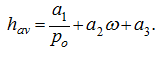 (17)
(17)