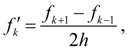Introduction

At solution of engineer-technical and other applied problems often happens it is necessary to find the certain order derivative from tabular given function . Besides sometimes by virtue of complexity of analytical expression of function its direct differentiation is too inconvenient. In these cases numerical differentiation is usually used. Here there is set of various receptions and ways [1 – 3].

One of the simplest formulas for calculation of function derivative is the formula of calculation of derivative through equidistant units [2, 3]:

(1)

where h – step, , .

Sometimes given function on interesting us segment [ a , b ] is replaced with some interpolating function , more often polynomial, and then is put [1]:

,        (2)

at .

Similarly higher orders derivatives of function are calculated.

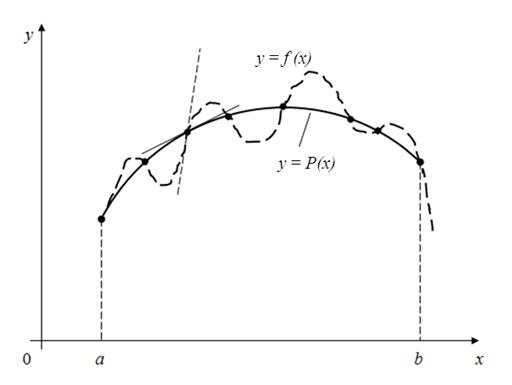
If an error of interpolating function is known:

,        (3)

then error of derivative is equal:

,        (4)

i.e. error of interpolating function derivative is equal to derivative of this function error . It is fair and for derivative of higher orders. Generally speaking, numerical differentiation is operation of less exact, than interpolation of function, differently affinity to each other ordinates of functions and on segment [ a , b ] yet does not guarantee affinity on this segment of their derivatives, i.e. a small divergence of angular coefficients of tangents to considered curves at the same values of argument (Fig.1).

Fig. 1. Difference in derivatives of given function y = f ( x ) and interpolating function y = P ( x )