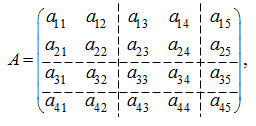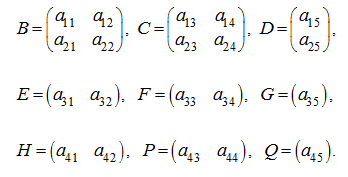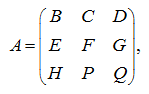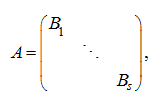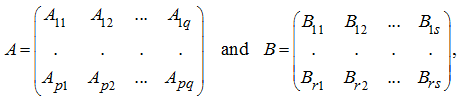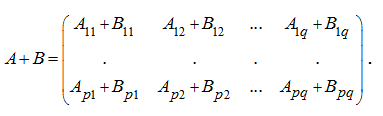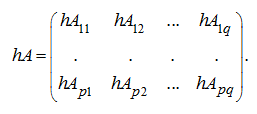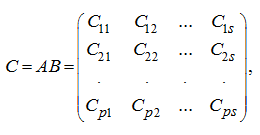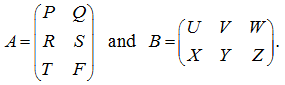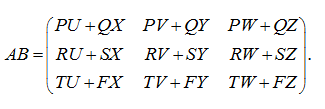Cellular matrices

Let's consider some matrix A and we’ll split it into matrices of lower order:

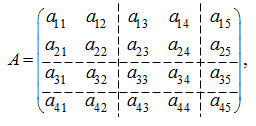
which are called cells or blocks .

Here cells (blocks) are matrices:

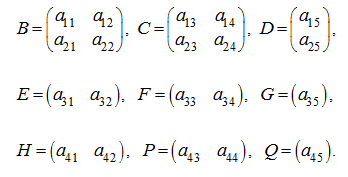
Now the matrix A can be considered as cellular or block matrix:

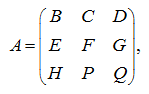
which elements are cells (blocks).

Apparently, that splitting of any matrix into cells (blocks) is maybe executed by various ways. In that specific case the cellular matrix can be quasi-diagonal one:

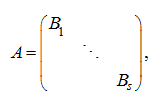
where cells 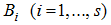– square matrices (generally speaking, of different orders), and outside of cells zeros are. Note, that
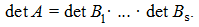
Cellular matrices of the same dimensions and with identical splitting are called conform .

Operations with cellular matrices are carried out by the same rules, as with usual matrices.

1. Addition and subtraction of cellular matrices

Let there are two conform cellular matrices:

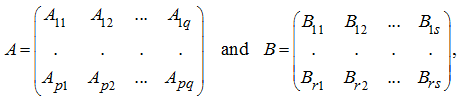
where p = r , q = s and cells 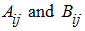of identical dimension. Then

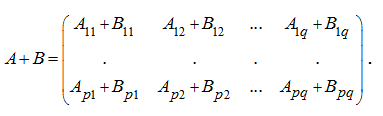
Subtraction of cellular matrices is carried out similarly.

2. Multiplication of cellular matrices

Multiplication of a cellular matrix to a number (scalar)

Let A – a cellular matrix and h – a number, then we have:

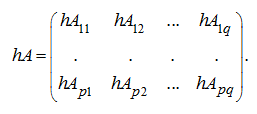
Multiplication of cellular matrices

Let's consider two conform cellular matrices:

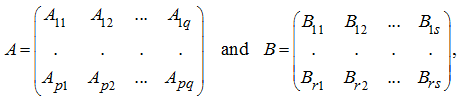
and q = r .

Let all cells 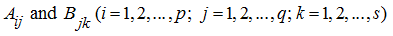such, that a number of columns of a cell 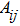is equal to a number of rows of a cell 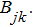(For example, apparently, that it takes place in that specific case, when all cells 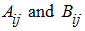– square matrices and have also the same order). Then it is easy to show, that a product of matrices A and B is too a cellular matrix:

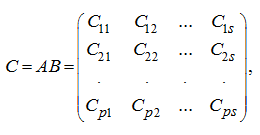
where 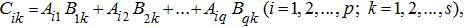that is multiplication of cellular matrices is similar to multiplication of numerical matrices [2].

E x a m p l e .  Multiply the cellular matrices

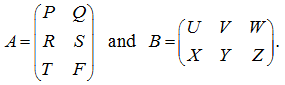
S o l u t i o n .
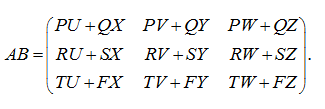