|
The spline interpolation
Lagrange’s, Newton’s and Stirling’s interpolation formulas
and others at use of big number of nodes of interpolation on all segment [
a
,
b
] often lead to bad approach because of accumulation of errors during calculations [2]. Besides because of divergence of interpolation process increasing of number of nodes not necessarily leads to increase of accuracy. For decreasing in errors all segment [
a
,
b
] is broken into partial segments and on each of them function
The piece-polynomial function certain on segment [ a , b ] and having on this segment a quantity of continuous derivatives is called spline. Advantages of spline interpolation in comparison with usual interpolation methods are in convergence and stability of computing process. Let's consider one of the cases most widespread in an expert – interpolation of functions by cubic spline.
Let continuous function
also we’ll designate
Spline
corresponding given function
1) on each of segments
2) function
3)
The third condition refers to as interpolation condition. The spline defined by conditions 1) – 3), refers to interpolation cubic spline . Let's consider a way of cubic spline construction [2].
On each of segments
where
Let’s differentiate (7) three times on х:
hence
From the interpolation condition 3) we recieve:
Besides we’ll consider
From conditions of function
From here in view of (7) we’ll receive:
Having designated
By virtue of matrix of coefficients is three-diagonal the system (9) has the unique solution [2].
Having found coefficients
Thus, the unique cubic spline, satisfying to conditions 1) – 3) exists and is found. |
Contents
>> Applied Mathematics
>> Numerical Methods
>> Interpolation of Functions
>> The spline interpolation
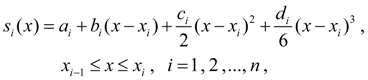
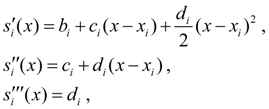
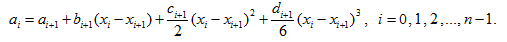
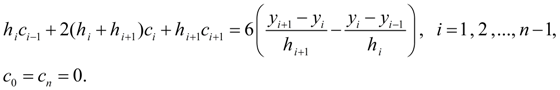 (9)
(9)
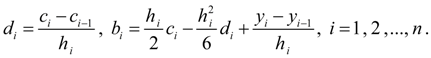 (10)
(10)