|
Introduction
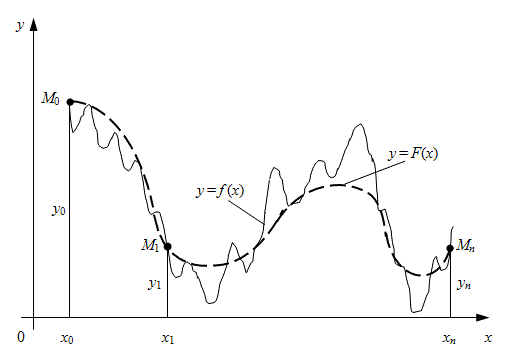
Interpolation
is an operation of approach of function given in separate points inside of some given interval. The elementary problem of interpolation consists in the following. On a segment [
a
,
b
]
n
+1 points
Fig. 1. Geometrical representation of function interpolation
In such statement the problem of interpolation, generally speaking, can have either uncountable set of solutions or not have at all solutions. However the problem it becomes unequivocal solved if instead of any function
Received interpolation formula
|
(
i
= 0, 1, 2, …,
n
) are given, named
nodes of interpolation
, and values of some function
in these points
It is required to construct the interpolating function
accepting in nodes of interpolation the same values, as
, i.e.
Vectorially it means (Fig. 1), that it is required to find some curve
of the certain type which are passing through the given set of points
.
to search a polynomial
of degree not above
n
, satisfying to conditions:
is used for approached calculation of values of the given function
for those
х
which are distinct from nodes of interpolation. Such operation refers to as
interpolation
of function