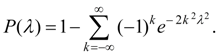|
Agreement Criteria For check of conformity of empirical distribution to theoretical (hypotheses) it is possible to impose a theoretical curve on the histogram (Fig. 6).
Fig. 6. Histogram and theoretical density function
Thus random divergences connected with the limited volume of supervision, or divergences testifying about wrong selection of leveling function (hypothesis) will inevitably be found out. For the answer this question so-called
«agreement criteria»
are used. For this purpose random variable
U
describing a divergence of empirical and theoretical distributions in the assumption of the validity of theoretical distribution is entered.
The measure of divergence
U
gets out so that function of its distribution
Sometimes act differently: in advance count a measure of a divergence
There is a set of agreement criteria among which the most common are
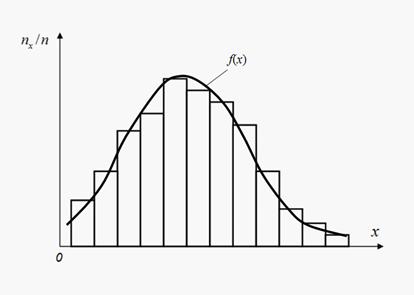
Pearson’s criterion
In
Pearson’s agreement criterion
where
k
– number of intervals of splitting of values of a random variable,
In practical problems it is recommended to have in each interval of splitting not less than 5-10 observations [3].
Let's designate through
t
number of the independent communications imposed on probability
1) Measure of a divergence
2) Number of degrees of freedom r = k – t is defined.
3) On
r
and
If this probability is rather small, the hypothesis (a theoretical curve) is rejected as improbable. If this probability is rather great, it is possible to recognize a hypothesis not contradicting the received experimental data. Be how much small owe probability р to reject or reconsider a hypothesis, is not solved on the basis of mathematical reasons and calculations. In practice if it appears, that р <0.1, it is recommended to check up or repeat experiment. If appreciable divergences will appear again, it is necessary to search for another law of distribution, more suitable for the description of empirical data. If the probability p > 0.1 (is rather great), it cannot be considered as the proof of validity of a hypothesis yet, and speaks only that the hypothesis does not contradict experimental data.
In
Kolmogorov-Smirnoff criterion
a measure of a divergence theoretical
F
(
x
) and empirical
A.N.Kolmogorov has proved, that at
aspires to the limit
For check of a hypothesis by Kolmogorov-Smirnoff criterion it is necessary to construct functions of distribution for theoretical
F
(
x
) and empirical
|
Contents
>> Applied Mathematics
>> Mathematical Statistics
>> Treatment of Experiment Results
>> Agreement criteria
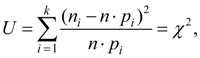
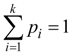 ). Thus, the scheme of application of criterion
). Thus, the scheme of application of criterion