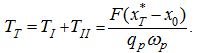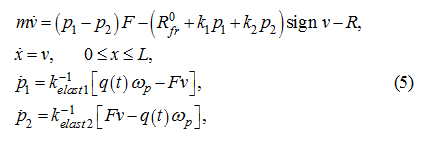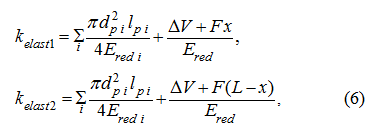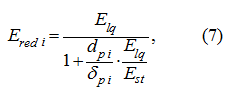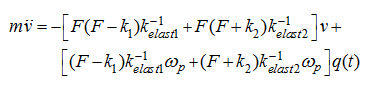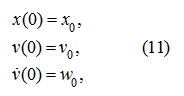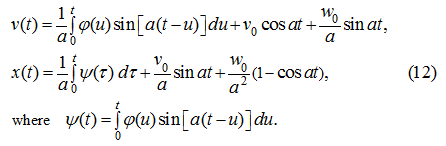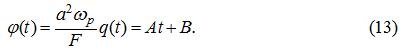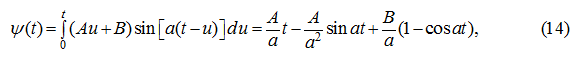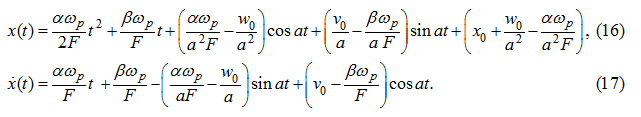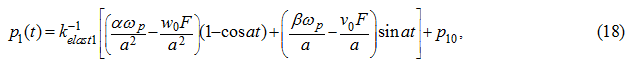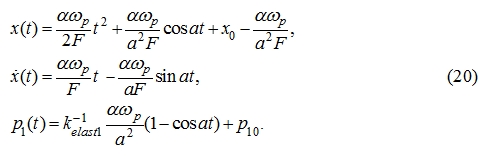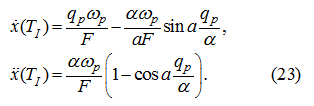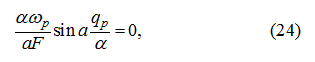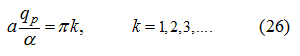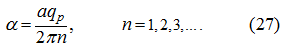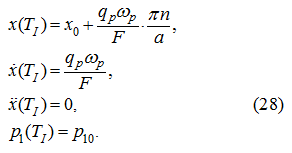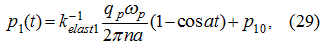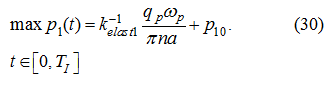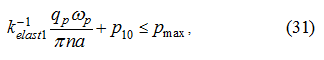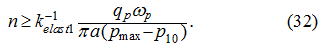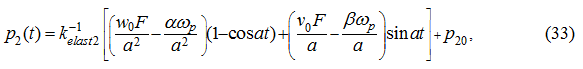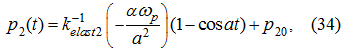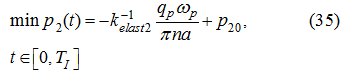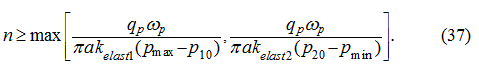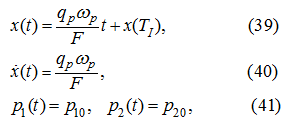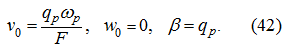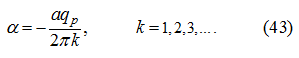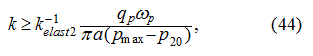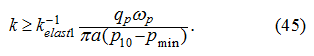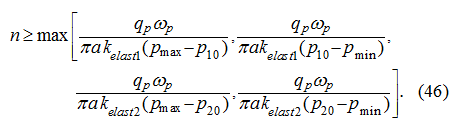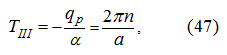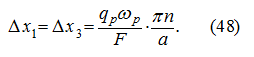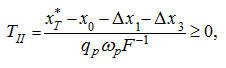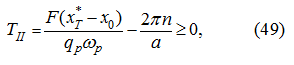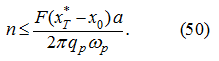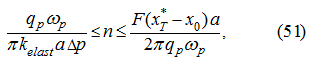Contents >> Engineering Mathematics >> Control Systems >> Dynamic Synthesis of Control System of Hydraulic Drive >> Synthesis of control by a power hydraulic drive of volumetric regulation >> Method of multiple periods of natural vibrations >> Algorithm

Control Systems - Dynamic Synthesis - Method of multiple periods of natural vibrations - Algorithm

Algorithm

Let's consider a simplified rated diagram of progressive hydraulic drive with the closed circulation of a stream presented on Fig. 3.

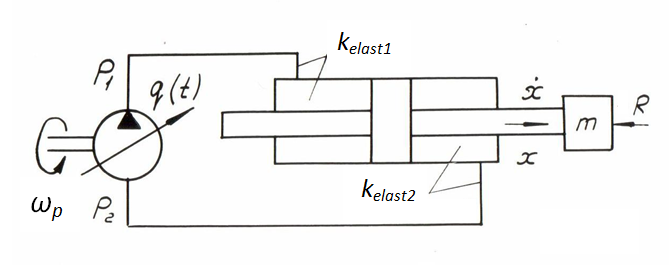
Fig. 3.

Let’s write system of differential equations of dynamics in view of elasticity of working liquid, accepting the following assumptions:
1). Leakages of working liquid in hydraulic system are absent, therefore work of boosting system is not considered.
2). Losses of pressure on length of pipelines and in local resistances negligible.
3). Reduced mass and load on the hydraulic cylinder rod, as well as frequency of rotation of the pump shaft are constant.
4). Parameters of working liquid (density, viscosity, module of volumetric elasticity) are constant.
5). Dynamics of the pump flow control mechanism is not considered.
The account of dynamics of the pump flow control mechanism does not represent basic difficulties, as this problem is maybe easily solved after (in parallel) considered, when required dependence of working volume of the pump q ( t ) (or even its current numerical value) is already known. For this purpose it is necessary to record mathematical model of the control system which output is q ( t ).
The mathematical model of considered hydraulic system (Fig. 3) in view of the accepted assumptions looks like:

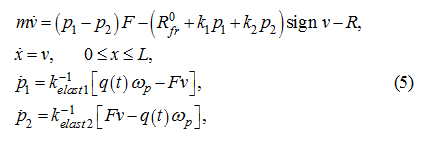
where m – reduced to a rod mass of mobile parts of the executive mechanism; р 1 , р 2 – pressures in pressure head and drain cavities of the hydraulic system; x , v – the hydraulic cylinder piston movement and speed; R 0 fr – a constant force of dry friction in sealing of the hydraulic cylinder at absence of pressure in cavities; k 1 , k 2 – factors of proportionality in variable components of force of dry friction, depending on pressure; R – a constant load on the hydraulic cylinder rod; ω p – an angular speed of the pump shaft; F – the working area of the hydraulic cylinder piston; q ( t ) – the pump working volume in function of time (actually a control signal); k elast 1 , k elast 2 – factors of elasticity of the hydraulic system cavities equal:

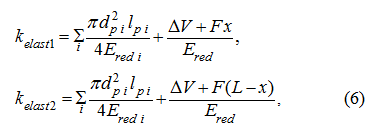
where L – the maximal stroke of the hydraulic cylinder piston; d р i , l р i – diameter and length of i -th pipeline; Δ V – a "dead" volume of the hydraulic cylinder cavity; Е red i – the reduced module of volumetric elasticity of i -th pipeline with a working liquid:

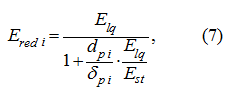
where E lq – module of volumetric elasticity of working liquid; δ р i – thickness of i -th pipeline wall; E st – the module of elasticity of the pipeline wall material; Е red – reduced module of elasticity of the hydraulic cylinder cavity, defined according to the formula similar (7).
Let's put for simplicity v > 0, that is sign v = 1.
Differentiating on time the first of equations of the system (5), in view of the accepted assumptions we’ll receive:

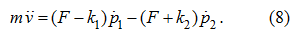
Substituting in (8) 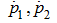from last two equations of the system (5), we’ll receive:

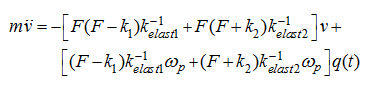
or

Despite of dependence (6) of factors of elasticity k elast 1 and k elast 2 on х , within the limits of the accepted assumptions and for actual values F , k 1 , k 2 and other parameters, it is easy to show (see the Appendix ), that the expression standing in the equation (9) as multiplier before v , changes slightly (~13 %), therefore as a first approximation it is possible to consider the equation (9) as linear:

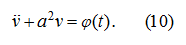
Having accepted the initial conditions:

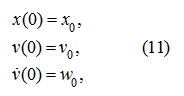
Let's receive the decision of the equation (10) which in view of initial conditions (11) looks like [9]:

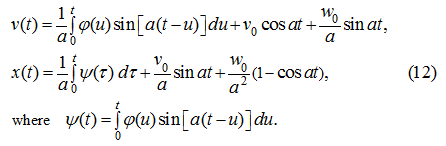
Proceeding from conditions of accuracy of positioning, it is necessary to choose control φ ( t ) so that by the end of regulation to extinguish natural fluctuations.
Let's consider a class of linear control φ ( t ) (generally – piecewise linear if to consider, that for each stage of movement the time interval (0, t ) is "sliding", that is its left border conforms t = 0; differently, initial conditions (11) for 2-nd and 3-rd stage of movement are replaced with values of phase variables in the end of the previous stage).
So, let q ( t ) = α t + β , then

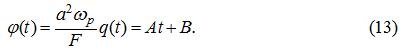
Substituting (13) in (12), we’ll receive:

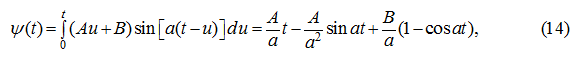
whence

or it is final:

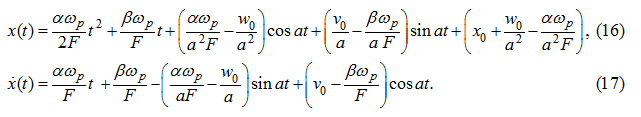
Substituting (17) in the equation (5) for р 1 and integrating on t , we’ll receive:

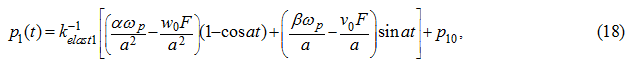
where р 10 = р 1 (0).
Let's consider separately the basic phases of movement and control.

Dispersal

The initial conditions at dispersal:

v 0 = 0, w 0 = 0,  β = 0.                   (19)

In this case we have:

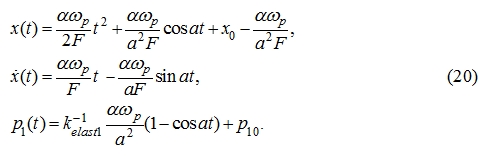
Let's enter the restrictions:

First of these restrictions (21) is entered, proceeding from requirements of hydraulic system operation (pressure should not be below some minimum level defined by conditions of suction of working liquid on the basic pump input) and failure of a pressure relief valve, otherwise a desirable control process by a hydraulic drive will be deformed. The restrictions (22) reflect purely geometrical opportunities of the variable displacement pump.
Let T I – time of control at dispersal, then T I = q p / α . At t = T I we’ll receive:

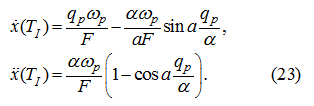
Let's demand, that 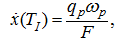then

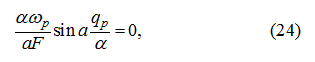
whence

and

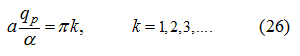
If to accept 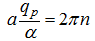(to ensure that, at the end of dispersal 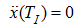), then

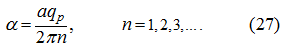
Then at t = T I we have:

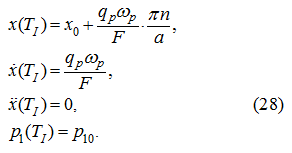
Let’s find max p 1 ( t ) at (27) on temporal segment 0 ≤ t ≤ T I :

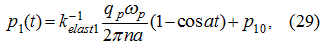
and as 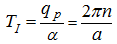– the period of function p 1 ( t ), then its maximum on [0, T I ] is equal:

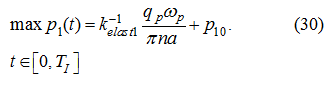
From the condition (21) we’ll receive:

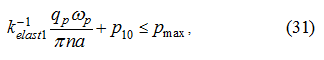
whence follows:

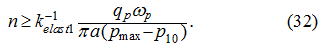
On the other hand, at absence of boost system pressure p 2 in a drain pipeline changes similarly (18):

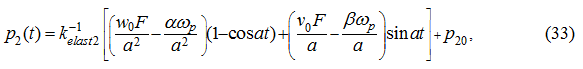
where p 20 = p 2 (0).
At dispersal, in view of the initial conditions (19), we’ll receive:

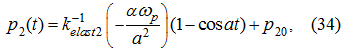
whence proceeding from the restriction (21) in view of (27), we’ll receive:

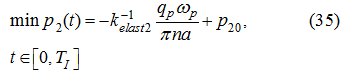
consequently,

Thus, from (32) and (36) follows, that at dispersal:

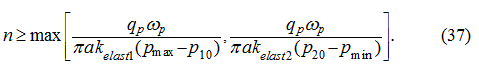
Once again we emphasize, that validity of formulas (34) – (37) takes place only at absence of boost system . At its availability there is no the need in these conditions.

Steady-state movement

For this stage of movement the new initial conditions are specified:

where 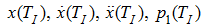– values of appropriating phase coordinates in the end of the previous stage of movement (dispersal).
Substituting (38) in the equations (16), (17) and (18), accordingly we’ll receive:

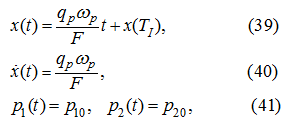
whence apparently, that on the temporal segment 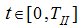an uniform movement of the hydraulic drive takes place. The value T II (duration of the steady-state movement) will be defined later.

Braking

The initial conditions at the stage of braking are:

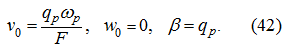
If to accept similarly (27) at dispersal, that at braking

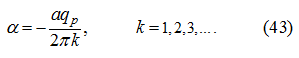
that substituting (42) in the equations (16), (17) and (18), we’ll receive from the condition (21) similarly previous:

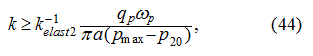
and

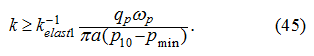
If to take as n and k their general meanings for all modes, then

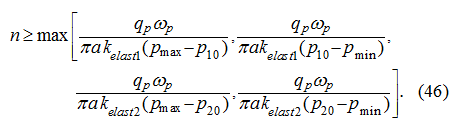
Duration of braking in this case will make:

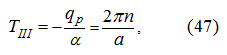
then movements of the piston at dispersal Δ х 1 and braking Δ х 3 are accordingly equal:

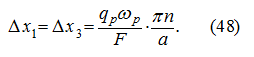
Then, if х Т * – the given final position of the piston,

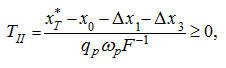
whence in view of (48) we’ll receive:

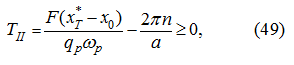
consequently,

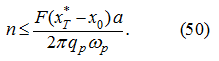
If to designate the right part of an inequality (46) through , then in view of (50) the inequality should take place:

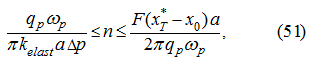
from which follows, that if it is not carried out (for example, at small movements 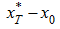) it is necessary to enter κq p instead of q p where 0 ≤ κ ≤ 1, that is to reduce q p until the inequality (51) will be carried out.
General time of movement Т is equal:

and the moment of the braking beginning is:
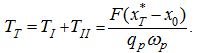
At t ≥ T III we’ll receive: α = 0, β = 0, v 0 = 0, w 0 = 0, that is the system "stops".
Let's note that from set of all admissible values n , that is satisfying the condition (46), it is necessary to choose the least one. It will allow under other equal conditions time minimizing of regulation Т , as well as will allow possibility to provide performance of the inequality (51).
On it the stage of "rough" control is ended.
The described control algorithm is illustrated on Fig. 4, where v ( t ) and x ( t ) – idealized cycle charts of speeds and movements of the executive hydraulic cylinder piston.

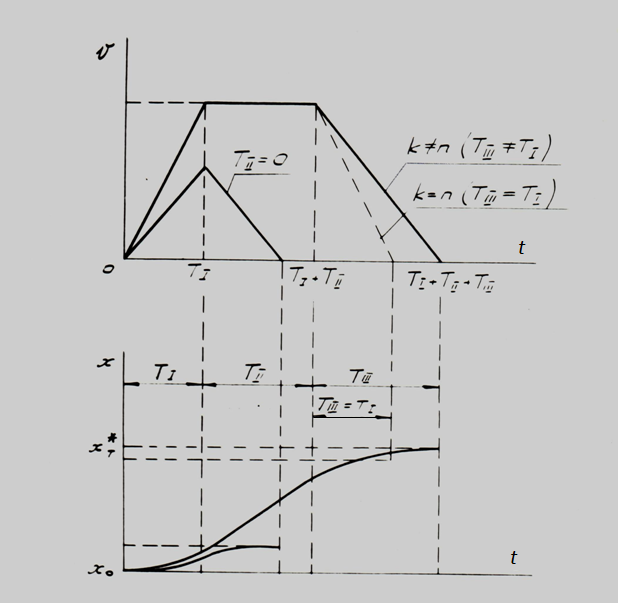
Fig. 4.


< Previous Contents Next >