|
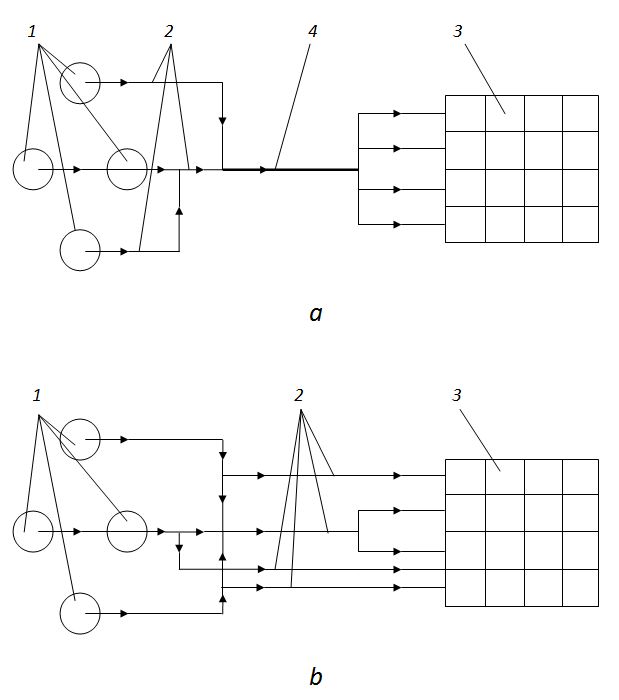
Structural analysis of the transport scheme The concrete mixing plants facilities on construction of large industrial objects represents the complex technological system consisting of a network of conveyor lines, storehouses concrete aggregates, departments of control screening, heating-cooling, dehydration, account bunkers.Two versions of technological schemes of supply of materials by conveyor transport from storehouses to account bunkers of concrete plants are possible (Fig.1).
Fig.1. Basic schemes of conveyor transport.
In the first case (Fig.1, a ) the materials coming from a storehouse or from group of storehouses, move to account bunkers by system of tape conveyors, and for this scheme availability of the main conveyor uniting all flows of materials is characteristic. In the second case (Fig.1, b ) the materials coming from storehouses, are not united in one flow, that is the main conveyor is absent.
Fig.2. Possible versions of transport routes.
Route
– the sequence of conveyors (Fig.2), transporting materials from same storehouse (for example,
m
1
= {
1, 2, 3, 4, 5, 6, 7
};
m
2
={
8, 3, 9, 10
}).
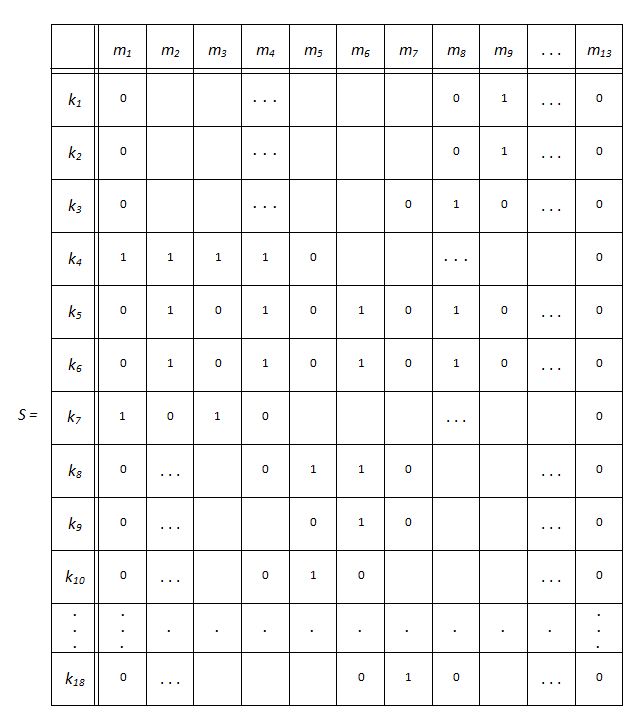
Fig.3. The actual scheme of conveyor lines of concrete mixing plants facilities. According this scheme aggregates of concrete (sand, gravel, road metal) various fractions move from storehouses C i by conveyor lines k l to concrete plants of cyclic ( I ) and continuous ( II ) action. In points A j and B j flowss of materials are accordingly divided or united. The initial information about structure of the considered transport scheme is shown in tab.1.
The scheme (Fig.3) and tab.1 provide a possibility of use of road metal at a plant of cyclic action as a aggregate for some marks of concrete. The structural analysis of the transport scheme we'll execute for its first version. To establish interconnection between separate routes, we'll draw up on the basis of tab.1 the following matrix S :
The matrix is constructed as follows. If on intersection of the
l
-th line and the
j
-th column of the matrix 1 is it means,
that the
l
-th conveyor line enters into the
j
-th route, otherwise the
lj
-th element of the matrix
S
is equal
to 0.
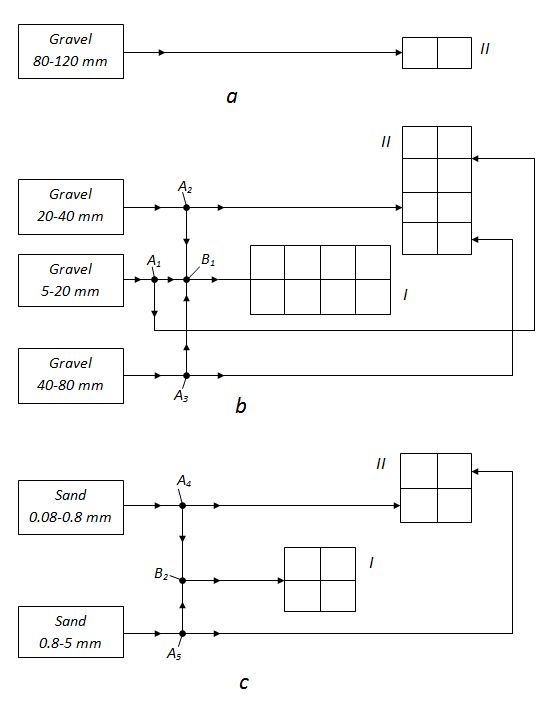
Fig.4. Technologically independent sites of the transport scheme. In the actual transport scheme it conforms to breakdown of the scheme on technologically independent three sites (Fig.4): transportation of gravel of fraction 80 - 120 mm - unit (Fig.4, a ); transportation of gravel of fractions 5 - 10, 10 - 20, 20 - 40 and 40 - 80 mm - network (Fig.4, b ); transportation of sand - network (Fig.4, c ).The control by transport flows of aggregate to account bunkers on three received sites can be carried out independently. |
Contents
>> Engineering Mathematics
>> Control Systems
>> Control of Flow-Transport System of Concrete Mixing Plants
>> Structural analysis of the transport scheme