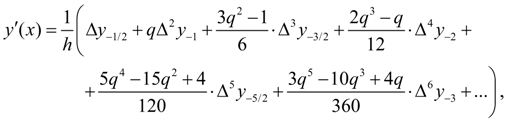|
Formulas of numerical differentiation
1. On a basis of Newton’s first interpolating formula
For finding of the first and second derivatives of function
Removing brackets and considering, that
we’ll receive:
Similarly, considering
we’ll receive:
In the same way if necessary, it is possible to calculate any order derivative of function. We’ll notice, that at calculation of derivatives in fixed point
х
as
It is possible to deduce also formulas of numerical differentiation based on Newton’s second interpolating formula [1].
2. On a basis of Newton’s second interpolating formula
Let
where for brevity of record the following designations are entered:
and so on.
From (8) in view of that
|
Contents
>> Applied Mathematics
>> Numerical Methods
>> Numerical Differentiaon
>> Formulas of numerical differentiaon
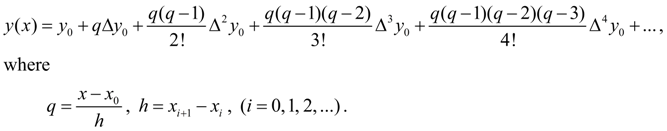
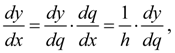
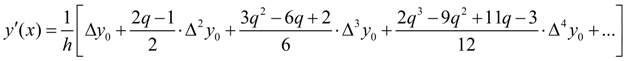
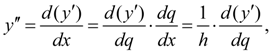
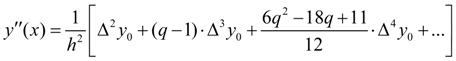
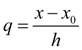 and replacing the function by Stirling’s interpolating polynomial, we’ll receive:
and replacing the function by Stirling’s interpolating polynomial, we’ll receive:

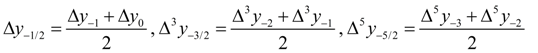
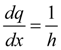 , follows:
, follows: