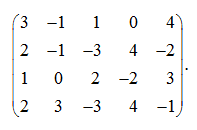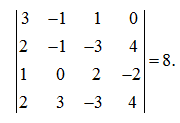Rank of a matrix

Let's consider a rectangular matrix:

If to choose in this matrix arbitrarily k rows and k columns, where 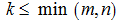then elements costing on an intersection of these rows and columns, form a square matrix of the k- th order. The determinant of this matrix is called a minor of the k -th order of a matrix A .

The rank of a matrix is the maximal order of a minor of a matrix not equal to zero.

Differently, the rank of a matrix A is equal r , if:
1) there is even one minor of the r -th order of a matrix A , not equal to zero;
2) all minors of the ( r +1)-th order and above are equal to zero or do not exist.

Rank of a zero matrix (a matrix consisting of zeros) is considered equal to zero.

The difference min ( m , n ) – r is called defect of a matrix . If defect of a matrix is equal to zero the matrix has the greatest possible rank.

E x a m p l e .  Define a rank of the matrix

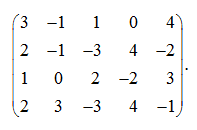
S o l u t i o n .  The left fourth order minor of the given matrix is equal to

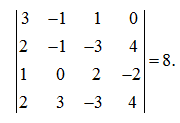
Consequently, the rank of the matrix is equal 4.