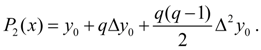|
Newton’s first interpolation formula
Let in equidistant points
Let's enter finite differences for sequence of values
Conditions (1) are equivalent to the equalities:
at
Lowering the transformations resulted in [1 ], we’ll finally receive Newton’s first interpolation formula :
where
The formula (3) is expedient for using for interpolation of function
In special cases we have: at n = 1 – formula of linear interpolation :
at n = 2 – formula of square-law or parabolic interpolation :
|
Contents
>> Applied Mathematics
>> Numerical Methods
>> Interpolation of Functions
>> Newton’s first interpolation formula
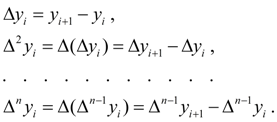
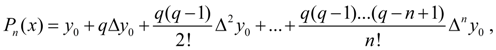
 – number of steps of interpolation from beginning point
– number of steps of interpolation from beginning point