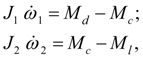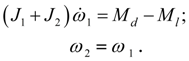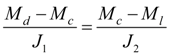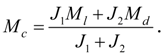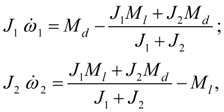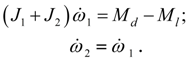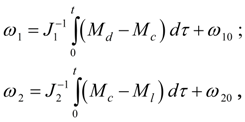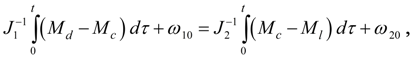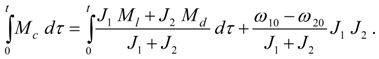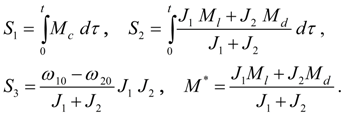Blocking of frictional clutches and hydraulic torque converters

Above (see the section «Introduction» ) it was marked, that feature of transient processes in mechanical and hydro mechanical drives is presence in blocked elements (frictional clutches and blocked hydraulic torque converters) two basic modes:

1) rotation of leading and conducted parts with slipping;

2) rotation of leading and conducted parts without slipping (a blocking mode).

The known solution of a problem of simulation of a blocking mode in mechanical drive with one blocked element [1, 5, 7], for a friction clutch, for example, is reduced [5] to a classical problem about dry friction model at zero speed of moving mass [6]. As to simulation drives with many blocked elements (as it takes place, for example, in modern hydro mechanical transmissions of mobile machines) this problem is interfaced to the certain difficulties as conditions of blocking of each blocked element depend on structure of the scheme, distributions of the external moments and the resulted moments of inertia, and also a mode of rotation of other blocked elements entering into the considered of a drive scheme.

At simulation of blocking mode of rotating masses of frictional clutches and blocked hydraulic torque converters it is possible to carry out joining of the sites neighboring on these elements, having united them in one site and to make recalculation of the resulted moments of inertia, having passed thus to system of the equations of lower order [1].

So, at the unblocked masses the system of the equations describing dynamics of clutch, looks like:

(36)

where resulted moments of inertia of the 1-st and the 2-nd sites adjoining, accordingly to leading and conducted parts of clutch; driving moment; moment transferred by clutch; the loading moment; angular speeds of leading and conducted parts of clutch.

At blocking the system of equations (36) is transformed to a kind:

(37)

However, at frequent change of blocking mode and the unblocked condition of clutch at such approach there is a number of the difficulties connected with possible and frequent change of structure of the scheme and the system of differential equations. Differently, the constant control of operating modes of these elements, recalculation of moments of inertia and acceptance of certain actions over change of the simplified scheme is required. It will lead to complication of algorithm of the solution and much greater time of calculations.

Below the method of forming of the equations is stated, allowing at simulation of dynamics of sites of the scheme irrespective of a condition of blocked masses to keep the constant structure of system of the equations. We’ll show, that transition from the equations of a kind (36) to the equations of a kind (37) is not obligatory as at correct definition of the moment it is possible to simulate both modes of a clutch rotation, using equations (36), not breaking that structure of the generated general system of equations.

Conditions of blocking of friction clutches and hydraulic torque converters. Let, , i.e. there was a blocking of leading and conducted parts of clutch. Then from (36) follows:

,    (38)

hence,

(39)

Substituting the expression (39) for into equations (36), we’ll receive:

(40)

whence follows:

(41)

Thus, if , then (39) takes place, and on the contrary. Hence, a condition of application of equations (36) in a blocking mode is performance of equality (39) and equality of angular speeds of leading and conducted parts of clutch .

Let's consider equality andfind out to what condition for the moments it is equivalent.

Let's integrate the equations (36) once on t and resolve them relatively :

(42)

where

From a condition of equality of speeds follows:

(43)

whence follows:

(44)

On the other hand, if (44) takes place then its substitution in the system (42) gives .

Thus, conditions and (44) are equivalent.

The analysis of blocking conditions of clutches. Let's enter the denotations :

(45)

Let the limiting moment developed by clutch a control signal, u – the external characteristic (for frictional clutch, for example, a control signal is pressure p ( t ) in the mechanism of pressing of disks of frictional pair , and the external characteristic – dependence of friction coefficient on a difference of angular speeds of disks). On Fig. 6 dependences of moments and angular speeds on time t are presented.

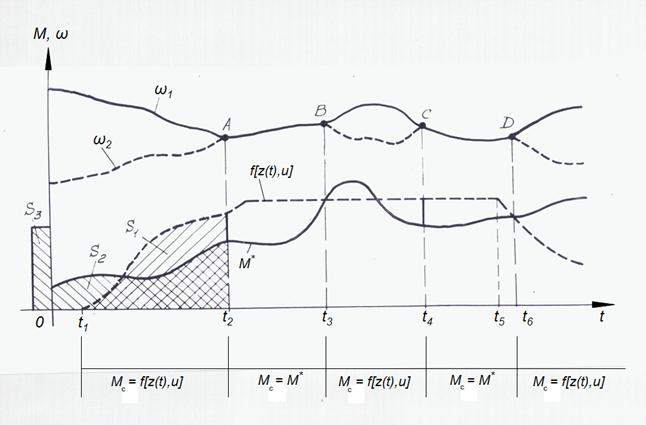
Fig. 6. Geometrical interpretation of clutch blocking mode.

At an equality of the areas under the moments curves (45) takes place, i.e. It simultaneously means alignment of angular speeds (point A). In this moment of time

(46)

therefore there will be a jump of the moment M _c with up to and the further movement of clutch disks on an interval will be blocked. At because of increase there comes moment, at which

(47)

and M _c to within a sign becomes equal to : i.e. a clutch slipping  ( , point B) begins. At the value of the moment falls up to value at which equality again takes place, i.e. (point C). As in this moment of time the condition (46) is again satisfied, there is a new jump M _c up to value and on an interval a clutch is again blocked. At a compulsory disconnection of clutch disks begins, the limiting moment decreases, and at again becomes less on the module, than . As a result at (point D) a clutch slipping again begins.

Blocking conditions (46) – (47) have been considered at record of mathematical models of a friction clutch (15) and a hydraulic torque converter (19) – (20).

For hydraulic torque converter with overtaking clutch always and blocking comes at , therefore blocking conditions of pump and turbine wheels for hydraulic torque converter (19) have some formal differences from blocking conditions of a friction clutch (15).